Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.10 - Ex. 9

Uma luz de rua é colocada no topo de um poste de 15   p é s . Um homem com 6   p é s de altura anda afastando-se do poste com uma velocidade de 5   p é s / s de acordo com uma trajetória reta. Com que velocidade se move o topo de sua sombra quando ele está a 40   p é s do poste?

Passo 1

Opa, bora lá! Vamos analisar o que nosso probleminha está falando.

Bom, ele nos diz que tem um carinha (que mora logo ali) com uma altura de 6   p é s e que anda com uma velocidade constante de 5   p é s / s se afasta de um poste de 15   p é s de altura e que produz uma sombra no chão. Sabendo disso, ele nos pede para determinar a velocidade da cabeça da sombra a partir do momento que o homem passa a 40   p é s pelo poste.

Tem ideia de como fazemos isso?

Bom... aqui temos um problema de taxa relacionada e o que temos que relacionar são as taxas da velocidade do topo da cabeça com a velocidade do carinha.

Para resolver esse problema podemos usar semelhança entre triângulos e definir uma variavel para a velocidade do carinha e a velocidade da sombra...

Assim, derivando a função em relação ao tempo e substituindo os valores do enunciado vamos resolver o problema

Veja só!

Passo 2

Vamos começar desenhando nosso problema...

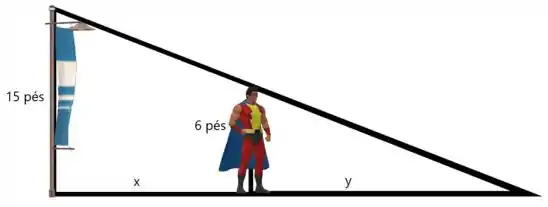
x é a distância do poste para o carinha e y a distância do carinha para o topo da sua sombra...

Por semelhança de triângulos temos que

x + y 15 = y 6

Vamos manipular essa função para isolar y em um lado da igualdade...

x 15 = y 6 - y 15

x 15 = y 10

y = 10 x 15

Tranquilo até aqui?

Passo 3

Conseguimos criar uma função de y em relação a x tanto x como y variam com o tempo.

Derivando com relação a t , temos

d y d t = d 10 x 15 d t = 10 15 d x d t

No enunciado foi dada que d x / d t que é a velocidade do carinha é de 5   p é s / s , ou seja

d y d t = 10 15 · 5 = 10 3

Porém esse não é a resposta final pois isso que encontramos é a variação de y , ou seja, a velocidade com relação ao carinha.

Com relação ao poste temos que v = d x d t + d y d t como podemos ver na figura do passo 2.

v = 5 + 10 3

v = 25 3   p é s / s

Prontinho! Entendeu tudo? Responde Aí!

Resposta

v = 25 3   p é s / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma frente fria aproxima-se de uma região. A temperatura é T graus t horas após a meia-noite e T = 0,1 400 - 40 t + t 20 ≤ t ≤ 4 Ache a taxa de variação de T em relação a t às 5h;
Estima-se que um empregado de uma firma que faz molduras para quadros possa pintar y molduras x horas, após começar o trabalho às 8 horas da manhã e y = 3 x + 8 x 2 - x 30 ≤ x ≤ 4 Ache a taxa segundo
O lucro de um varejista é $ 100 ⋅ y quando são gastos diariamente $ x em propaganda e y = 2500 + 36 x - 0,2 x 2 Use a derivada para determinar se seria lucrativo aumentar a verba de propaganda, consid
Se C(x) for o custo total da fabricação de x pesos de papel e C x = 200 + 50 x + x 2 5 Ache a função custo marginal;Ache o custo marginal quando x = 10.
Um balão mantém a forma de uma esfera enquanto está sendo inflado. Ache a taxa de variação da área da superfície com respeito ao raio no instante em que o raio for 2 m.