Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 2
Como escolher dois números não negativos tais que sua soma seja e a soma de seus quadrados seja
(a)a menor possível
(b)a maior possível
Passo 1
Temos os números e , não negativos. Sua soma vale . Escrevemos isso:
Agora, em um problema de otimização, queremos as condições pra soma de seus quadrados pedidas em (a) e (b). Também escrevemos isso, na forma de uma função:
Só que não é prático trabalharmos com funções de duas variáveis. Podemos fugir disso escrevendo em função de , a partir da primeira equação. Dela, podemos escrever:
Passo 2
Agora, substituímos essa sentença pra em , e vamos resultar em uma :
Desenvolvemos esse expoente, que é um produto notável relativamente simples:
Como temos um problema de otimização, agora derivamos essa função e igualamos a derivada a zero. Assim, vamos ter os pontos críticos.
Passo 3
Igualamos a zero:
Esse é nosso ponto crítico. Como fazer pra saber se é de máximo ou de mínimo? Calculamos a derivada segunda!
Sendo o resultado positivo, a função tem concavidade voltada pra cima, e então é ponto de mínimo. Sendo negativo, concavidade voltada pra baixo, e então é ponto de máximo. Temos:
Sendo positivo, é ponto de mínimo.
Passo 4
Se , determinamos facilmente:
Então, esse é o par cuja soma dos quadrados é a menor possível, o que responde a letra (a).
Pra respondermos a letra (b), o gráfico da função vai nos ajudar:
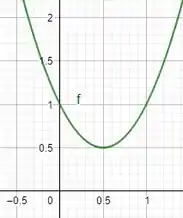
Já sabemos que o par ordenado ( nos dá e cuja soma dos quadrados é a menor possível.
Lembre que outra condição do exercício é de que e sejam não negativos. Então, na realidade, estamos trabalhando em um intervalo dentro dessa função, sendo ele .
Então, podemos dizer que o par ordenado é o “limite” da nossa parábola, sendo o extremo do nosso intervalo.
Assim, por ser o extremo do intervalo, onde sabemos que se passa por um ponto de mínimo, e que não há outro extremo (pois vai a infinito), esse par vai conter os valores de e cuja soma de seus quadrados seja a maior possível!
Logo, e são os números que atendem a condição da letra (b). Se você tiver tempo, tome alguns números positivos cuja soma dê 1, some seus quadrados e verifique que o resultado será sempre menor que:
Resposta
(a)(
(b)