Primeiro, vamos começar entendendo qual nossa região de integração. Para isso precisamos olhar os limites de integração para cada variável dada na nossa integral:

Então, vamos ter as seguintes variações:

Então, o que precisamos fazer é escrever nossa integral em outras 5 ordens diferentes de:

Mudando sempre que necessário os limites de integração para cada variável. Para isso vamos precisar visualizar melhor esse sólido e suas projeções nos planos e .

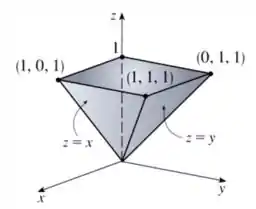
Sólido descrito

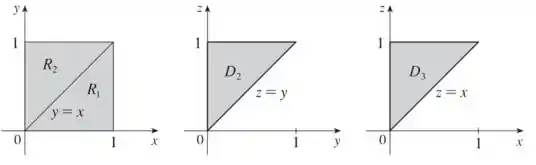
Projeção desse sólido nos planos , e

Veja que no plano temos a projeção cortada pela reta , então dividimos em e . Vamos então reescrever essas integrais.

• :

Vamos imaginar que vamos nos movimentar ao longo do eixo . Assim, podemos dividir nosso sólido em duas partes: o sólido vermelho e o verde da figura. Para o sólido verde, temos que:

Para o sólido vermelho, temos que:



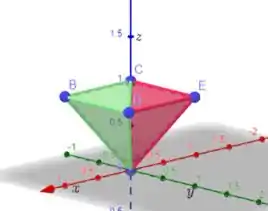
A projeção do sólido verde, no plano , é a região , enquanto que do sólido vermelho é a região .



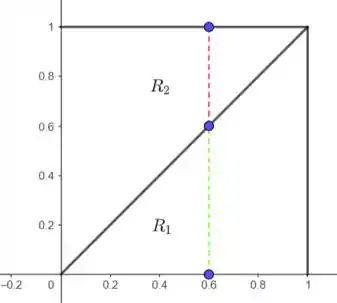
Regiões e

Para a região (reta verde da figura acima), temos que

Para a região (reta vermelha da figura acima), temos que:

Dessa forma, temos que a integral pode ser reescrita como:

Passo 4

• :

A idéia será a mesma que a anterior, ou seja, dividimos o sólido em dois (verde e vermelho). A única coisa que vamos precisar mudar é como vemos as regiões e :



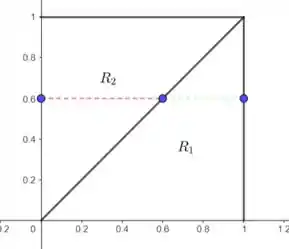
Para (reta verde da figura acima):

Para (reta vermelha da figura acima):

Dessa forma, a integral fica:

Passo 5

• :

Vamos imaginar que podemos nos movimentar sobre o eixo . Nesse caso, ficamos sempre limitados entre , concorda? A projeção será a região no plano .



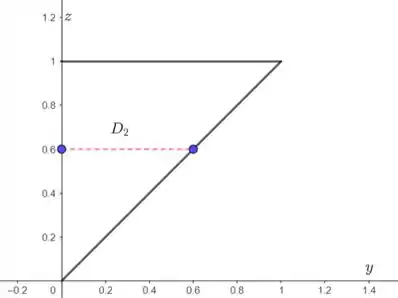
Observe que temos:

Logo, a integral pode ser escrita como:

Passo 6

• :

Vamos imaginar que podemos nos movimentar sobre o eixo . Nesse caso, ficamos sempre limitados entre , concorda? A projeção será no plano , o que representa . Veja:



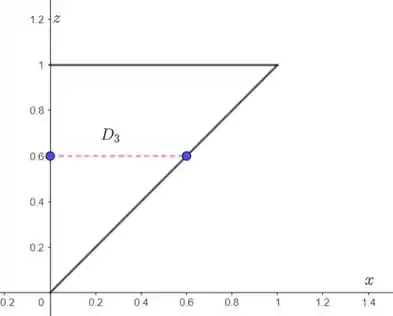
Assim, temos que:

Segue que a integral é:

Passo 7

O raciocínio é o mesmo do item anterior.

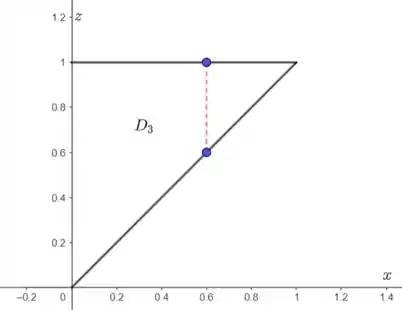
Observe que devemos ter:

Logo, a integral é: