Expresse a integral como uma integral iterada de seis modos diferentes, onde E é o solido limitado pelas superfícies dada.
Passo 1
Faala, galera!
Nessa questão precisamos expressar uma integral de seis formas diferentes!
Mas... que formas são essas?
Lembra que uma integral tripla a gente integra sempre de dentro pra fora, seguindo a ordem dos diferenciais:
Essa ordem pode ser feita de seis formas diferentes! Isso tem a ver com a permutação desses três elementos, que da , mas não se preocupa que não vamos precisar usar análise combinatória aqui não haha
O que a gente vai precisar é do conceito de regiões do tipo , e :
- Região do tipo é quando o está entre duas funções de e , onde é a projeção da região no plano .
- Região do tipo é quando o está entre duas funções de e , onde é a projeção da região no plano .
- Região do tipo é quando o está entre duas funções de e , onde é a projeção da região no plano .
Uma integral sobre uma região do tipo é calculada assim:
Sendo que esse pode ser ou .
A integral fica:
E o é ou
Nesse caso, a integral é:
Com o sendo ou
Pra cada um desses tipos, a gente consegue escrever a integral de dois modos diferentes, totalizando seis!
Então vamos descrever nossa região como cada um desses tipos, e assim conseguimos determinar os seis jeitos de escrever a integral!
Uma observação que pode facilitar nossa vida:
Quando a gente tem uma integral múltipla, existe uma regrinha pra ordem das variáveis. Se os limites de integração de uma variável dependerem da outra, a variável que depende tem que estar mais pra dentro.
Sem ferir essa regra, a gente pode mudar a ordem das variáveis a vontade!
Parece muita coisa, mas vamos com calma que vai sair!
Passo 2
Primeiro, vamos descrever como uma região do tipo .
Vamos começar desenhando nosso sólido, que é um cilindro entre dois planos:
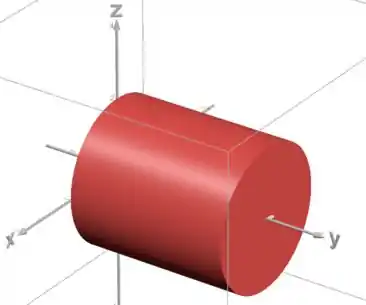
Pra descrever esse sólido como uma região do tipo , a gente precisa isolar o na equação da superfície do cilindro:
Essas duas equações representam a parte de cima () e de baixo () da superfície do cilindro. Como nosso sólido está entre essas duas partes da superfície:
Agora vamos olhar a projeção no plano :
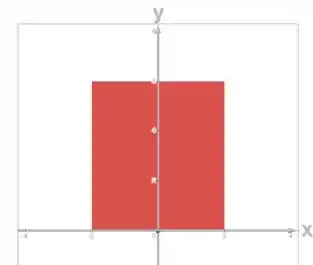
Como é um retângulo, temos:
Então a primeira forma da integral fica:
Passo 3
Agora vamos perceber uma coisa importante.
Nessa integral, a única dependência dos limites das variáveis é que os de dependem de .
Então só precisamos nos preocupar com deixar a integral de antes da de . Com isso, conseguimos mais duas formas da integral:
Trocando e :
Ou trocando e :
Passo 4
Só faltam três integrais!
Pra achar, vamos descrever nosso sólido agora como uma região do tipo :
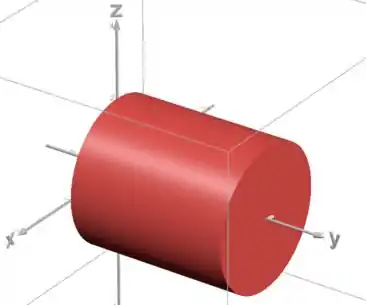
Isolando o na equação do cilindro:
De forma equivalente com o tipo , essas duas equações são as partes da superfície para e . Como o sólido está entre as duas:
E a projeção no plano :
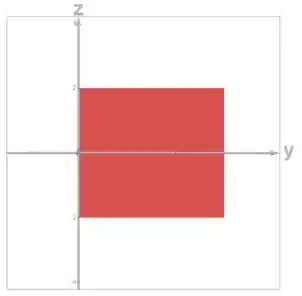
Temos um retângulo com:
Então:
Passo 5
Da mesma forma que fizemos no passo 3, vamos trocar as variáveis de lugar pra achar as últimas duas integrais.
Só precisamos tomar cuidado pra deixar a integral de antes de :
Trocando com :
Trocando com :