Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.7 - Ex. 28
Expresse a integral como uma integral iterada de seis modos diferentes, onde E é o solido limitado pelas superfícies dada.
Passo 1
E aii, pessoal!
Essa questão pede pra gente expressar uma integral de seis formas diferentes.
Como assim??
Bom, o que vai mudar nessas seis formas é a ordem de integração, que é definida pelos diferenciais no final da integral:
Pra isso, a gente precisa relembrar um conceito importante, que é regiões dos tipos :
- Região do tipo é quando o está entre duas funções de e , onde é a projeção da região no plano .
- Região do tipo é quando o está entre duas funções de e , onde é a projeção da região no plano .
- Região do tipo é quando o está entre duas funções de e , onde é a projeção da região no plano .
Uma integral sobre uma região do tipo é calculada assim:
Sendo que esse pode ser ou .
A integral fica:
E o é ou
Nesse caso, a integral é:
Com o sendo ou
Pra cada um desses tipos, existem duas formas diferentes de escrever a integral. Ou seja, no total são os seis que a questão quer!
Então vamos descrever o nosso sólido como região de cada um dos tipos e determinar as integrais!
Relaxa, que a gente só precisa escrever a integral, não vamos calcular nenhuma! Então é um pouquinho mais tranquilo do que parece 😅
Passo 2
(1) Região do tipo
Nosso sólido é limitado por:
(que são os planos e )
Desenhando isso, chegamos nesse sólido:
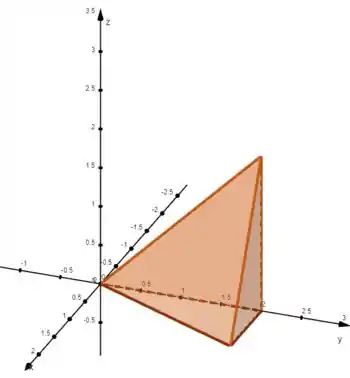
A face que aparece na direita desse desenho é o plano , e a face de “cima” é o plano (que é a reta no plano e a reta no plano ).
Assim, conseguimos ver que o sólido está abaixo dessa face e acima de :
Passo 3
Com relação a e , vamos ver a projeção no plano :
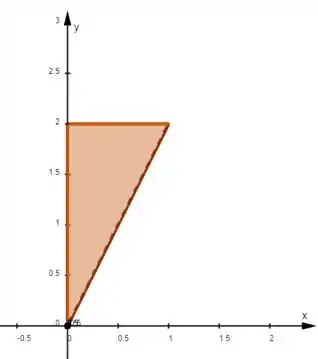
A região está acima da reta e abaixo da reta :
E o varia de a
Com esses limites, montamos a integral:
Podemos inverter esse se isolarmos o na equação da reta:
Agora vemos que a projeção do sólido está entre e :
E varia de a :
Passo 4
(2) Região do tipo
Pra descrever como uma região do tipo , vamos agora isolar o :
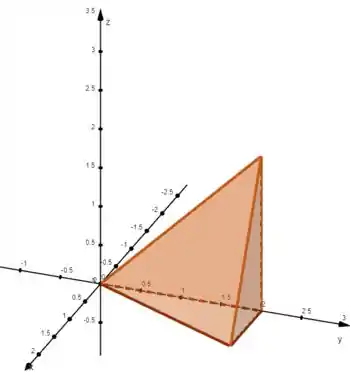
Agora olhando por , o sólido está entre e essa face, então:
Passo 5
Olhando pra projeção no plano :
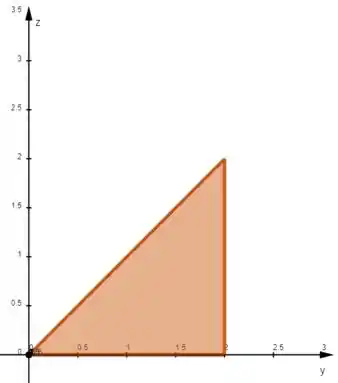
A região está entre o eixo e essa reta:
Então
E para :
A integral fica:
Igual fizemos em (1), pra inverter :
A região está entre e :
E o varia de a
Então a outra forma da integral fica:
Passo 6
(3) Região do tipo
Pra descrever como uma região do tipo , vamos isolar o na equação:
Voltando pro sólido:
Percebe que olhando com relação a , o sólido está entre a face de cima () e a face da direita ():
Passo 7
Agora olhando pra projeção no plano , pra vermos os limites de e :
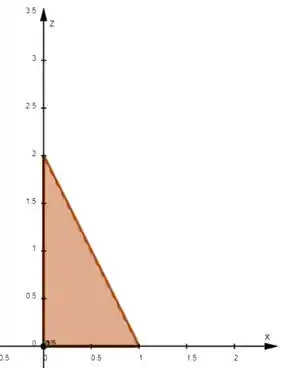
A projeção está limitada por essa reta, que é
Então:
E
E a integral fica:
De novo, pra inverter :
A região está entre essa reta e :
E: