Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 7

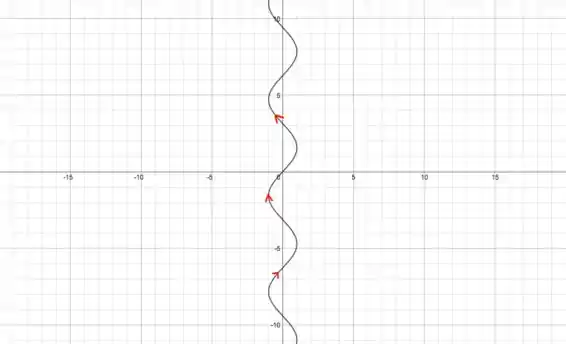
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce.

r t = < sin ⁡ t ,   t >

Passo 1

Queremos esboçar o gráfico da seguinte função paramétrica, mostrando a direção em que o parâmetro cresce:

r t = < s e n t , t >

Aqui iremos passar a curva para coordenadas cartesianas para melhor visualizarmos os comportamentos da nossa curva. Iremos fazer isso igualando y = t e substituindo o valor de t em x = sin ⁡ t .

Após fazermos isso, poderemos entender o comportamento da nossa função. Para plotar o gráfico, iremos utilizar o GeoGebra, pois é melhor do que você me ver desenhando a mão hehe.

Mas veja, para plotar um gráfico em função de t você pode criar uma tabela com valores distintos de t e os respectivos valores de x t e y t , e assim poderemos plotar esses pontos no papel e termos o gráfico.

Temos que

x = sin ⁡ t

E

y = t

Sendo assim, o que a gente tem em coordenadas cartesianas é:

x = sin ⁡ y

Passo 2

Com a equação paramétrica, temos as seguintes informações:

x = s e n t ,     ( 1 )

y = t ,     ( 2 )

Aplicando a equação ( 2 ) em ( 1 ) :

x = s e n ( y )

No gráfico abaixo a gente pode visualizar:

x = sin ⁡ y é a curva desenhada em preto

y = x é a curva pontilhada vermelha.

e

y = sin ⁡ x é a curva pontilhada azul.

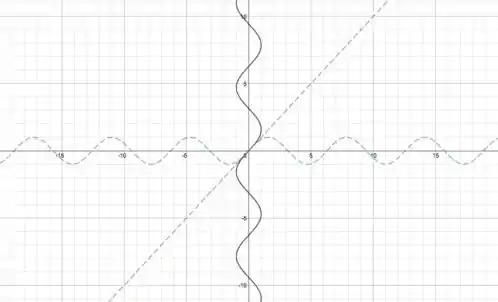
Conforme t cresce, y também aumenta logo o parâmetro vai indo para cima.

Assim:

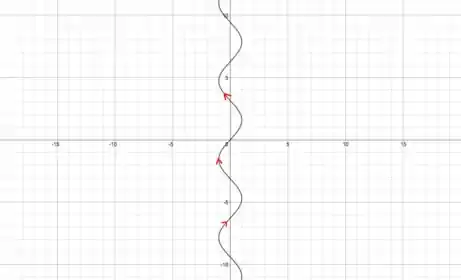
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o comprimento da curva dada. r t = t , 3 cos ⁡ t ,3 sen ⁡ t ,- 5 ≤ t ≤ 5 ATENÇÃO: O enunciado do livro é t , cos ⁡ t ,3 sen ⁡ t , mas com esse r ( t ) se chega numa integral que não é possív
Determine o comprimento da curva dada.r (t) = 〈2 t , t^2 , (1)/(3) t^3〉 , 0 = t = 1
Mostre que o plano osculador em cada ponto da curva r t = t + 2,1 - t , 1 2 t ² ² é o mesmo plano. O que você pode concluir sobre a curva?
Utilize um computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva. r t =c o s 2 t , c o s 3 t , c o
Trace a curva com equações paramétricas x = s e n t , y = s e n 2 t , z = c o s 4 t . Explique sua forma representando por gráficos suas projeções para os três planos coordenados.