Determine se o conjunto dado é ou não: (a) aberto, (b) conexo e (c) simplesmente conexo.
Passo 1
Faala, turma, como vocês estão?
Esse exercício pede pra gente explorar as definições de conjunto aberto, conexo e simplesmente conexo, em um conjunto:
Vamos lembrar o que é isso:
- Aberto: para todo ponto do conjunto existe uma bola aberta centrada nesse ponto que esteja inteira no conjunto.
- Conexo: quaisquer dois pontos no conjunto podem ser ligados por um caminho inteiro dentro do conjunto.
- Simplesmente conexo: é conexo, e qualquer curva fechada contorna só pontos que estejam dentro do conjunto.
Na prática, quer dizer que as curvas que limitam o conjunto não pertencem a ele:
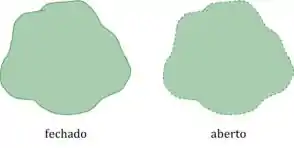
Na prática, o conjunto não é constituído de dois ou mais pedaços separados.
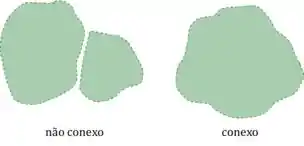
Na prática, além de ser conexo, não tem nenhum buraco no conjunto.
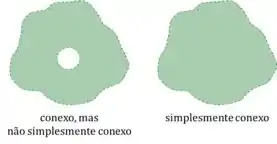
Vamos olhar primeiro pro desenho do nosso conjunto. Daí, verificamos pra cada uma dessas definições se ele se encaixa ou não.
Bora...
Passo 2
Nosso conjunto é
Po, esse indica que é uma região circular né?
Estamos entre uma circunferência de raio e outra de raio , mas elas mesmas não estão incluídas:
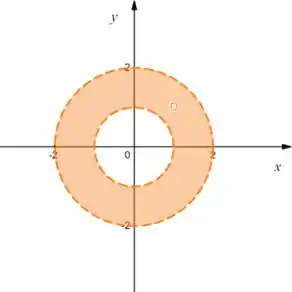
Passo 3
(a)
As curvas que limitam o conjunto são as circunferências de raios e . Como elas mesmas não fazem parte do conjunto:
Sim, o conjunto é aberto.
Passo 4
(b)
Sobre ele ser conexo, a gente vê pelo desenho que o nosso conjunto é um só, ou seja, não é dividido em dois ou mais pedaços. Então:
Sim, o conjunto é conexo.
Passo 5
(c)
Agora temos um problema... percebe que nosso conjunto é um círculo de raio com um buraco (um círculo de raio ) no meio. Isso quer dizer que o nosso conjunto não é “inteiro”, ele tem um buraco e:
Não, o conjunto não é simplesmente conexo.
Resposta
- Sim
- Sim
- Não