Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.4 - Ex. 7
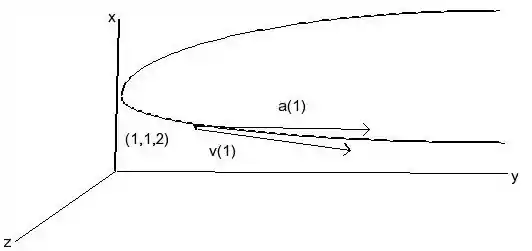
Determine a velocidade, a aceleração e a velocidade escalar da partícula cuja função posição é dada. Esboce a trajetória da partícula e desenhe os vetores velocidade e aceleração para os valores de especificados.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte equação da posição de uma partícula:
Queremos calcular a velocidade, a aceleração e a velocidade escalar da partícula.
Para isso, basta sabermos que a velocidade é a derivada da posição em função do tempo. E que a aceleração é a derivada da velocidade em função do tempo.
A velocidade escalar vai ser o módulo do vetor velocidade que a gente vai descobrir 😉
Vamos colocar isso de forma matemática no Passo 2.
Aah... também queremos esboçar a trajetória da partícula e desenhar os vetores velocidade em .
Passo 2
Uma partícula que tem uma função vetorial de posição do tipo:
Tem como função vetorial velocidade:
Velocidade escalar:
E vetor aceleração:
Passo 3
Queremos calcular o vetor velocidade, velocidade escalar e aceleração, e após isso, esboçar a curva da seguinte função vetorial, desenhando o vetor aceleração e posição no ponto:
O vetor posição em é:
Vamos calcular a velocidade:
Em :
Passo 4
A velocidade escalar da partícula é:
Passo 5
O vetor aceleração da partícula é:
Em :
Passo 6
Para esboçar a curva, vamos transformar a equação paramétrica em equação cartesiana:
Aplicado a equação em :
Então temos:
O gráfico dessa equação é:
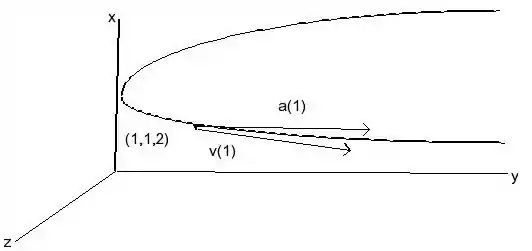
Resposta
