Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 13.2 - Ex. 31
Atirando um projétil em um declive Um projétil ideal é lançado diretamente ao longo de um plano inclinado, conforme mostrado na figura a seguir.
a. Mostre que o maior alcance no declive é atingido quando o vetor velocidade inicial bissecta o ângulo AOR.
b. Se o projétil fosse atirado em um aclive em vez de um declive, que ângulo maximizaria seu alcance? Justifique sua resposta.
Passo 1
Fala minha galera querida!! Vamos desenhar as figuras de cada caso para entender do que se trata.
-
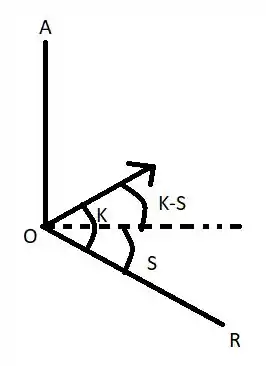
α = K e S os ângulos do lançamento: -
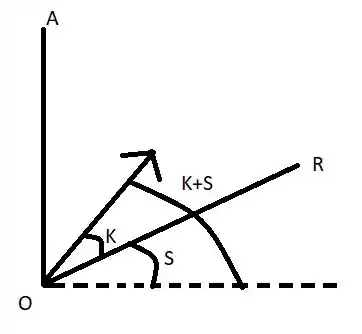Vamos desenhar a figura para esse caso com aclive.
Passo 2
Vamos começar descobrindo o tempo em que o projétil atinge o declive, para demonstrar que o maior alcance é obtido com o projétil lançado da bissetriz do ângulo.
Da figura, tiramos que , vamos guardar essa informação.
Das equações dos lançamentos temos:
Como R está abaixo da posição 0 do eixo, então .
Vamos reescrever a tangente.
Rearranjando, descobrimos que o tempo é:
Passo 3
Vamos descobrir o x máximo, derivando a função x da posição em relação ao ângulo K, depois de substituir o tempo encontrado.
Lembrando que
E está demonstrado que o maior alcance é obtido pela bissecção do ângulo.
Passo 4
Pessoal, a letra b temos que fazer a mesma coisa, só vai mudar o sinal no final, vamos ver.
Passo 2
Vamos começar descobrindo o tempo em que o projétil atinge o aclive, lá no topo de R.
Da figura, tiramos que , vamos guardar essa informação.
Das equações dos lançamentos temos:
Vamos reescrever a tangente.
Rearranjando, descobrimos que o tempo é:
Passo 3
Vamos descobrir o x máximo, derivando a função x da posição em relação ao ângulo K, depois de substituir o tempo encontrado.
Lembrando que
Caso fosse atirado de um aclive, este é o ângulo que maximizaria seu alcance!
Bora pro próximo!
Resposta
- Demonstração.