Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.2 - Ex. 43
- Escreva uma equação cujo gráfico seja o eixo . Escreva uma equação cujo gráfico seja o eixo . Escreva uma equação cujo gráfico seja o conjunto de todos os pontos no eixo ou .
Passo 1
- Quando vemos uma função desde o inicio da matemática vemos algo do tipo
- Aqui queremos então a equação para o eixo y. Isso quer dizer que queremos uma reta vertical no ponto zero de x, certo? Podemos usar o mesmo a mesma ideia do item a)
- A equação nesse caso pode ser . Pode ser ate uma solução tirada da cartola, mas se liga só. Você conhece a função abaixo ?
Por exemplo
Existe outras formas da gente escrever isso. Se por exemplo é um número qualquer.
É uma forma de escrever uma função. Como também
Descreve outra função. Estamos trabalhando com um polinômio de grau 1. Isso quer dizer que estamos falando de retas. é uma reta de ângulo . Enquanto é uma reta constante e deitada. Com ângulo . Agora quando usamos a forma estamos querendo então dizer que nossa reta é vertical, com ângulo de
Nossa letra a) pede a equação da reta do eixo x. Isso quer dizer que queremos uma reta horizontal na altura Zero de . Então não seria nada mal se escrevêssemos uma equação assim :
Não é mesmo? E é essa mesma a equação do eixo x
Passo 2
E prontinho essa equação nos da a reta vertical do eixo y.
Passo 3
Se não conhece tranquilo, vou plotar pra você.
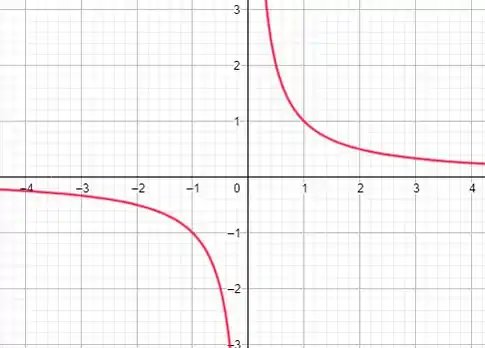
Se fizer o seguinte
Nos dá o mesmo gráfico certo? Se formos variando o numero que igualamos nossa função vamos ver que essas 2 curvas ou se afastam ou se aproximam. Inclusive é um ótimo exercício. Ficar brincando com a calculadora gráfica e ver como as funções se comportam.
Se fizermos vemos que tem as curvas mais próximas. E cada vez mais próximas quanto menor o número. O legal acontece quando igualamos a zero. As curvas se juntam num ângulo reto. E formam os eixos coordenados.