Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 2.5 - Ex. 1a
- Escreva a equação e identifique a seção de cada superfície quadrica no plano indicado
Passo 1
Oiii a todos que estão ingressando no mundo do cálculo de várias variáveis. Quando aprendemos a fazer gráficos em cálculo 1, aprendemos vários truques. Inclusive, se você já está mais sagaz, de olhar para uma função e concluir “ah isso aqui, tem um jeito de círculo”, por exemplo, rs. Se você ainda não pegou essa sagacidade, relaxe! Isso vem apenas com o tempo e após vários exercícios.
Uma dica que dou é usar muito uma calculadora gráfica. Isso ajuda absurdamente na compreensão da geometria do seu sistema.
Passo 2
Estamos trabalhado com a função
Se formos plotar esse grafico vamos observar um elipsoide
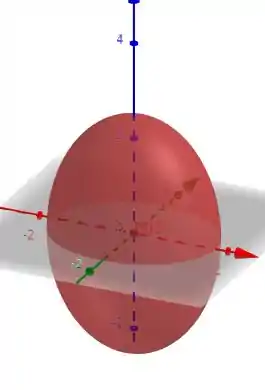
O que vamos fazer agora é um corte com o plano
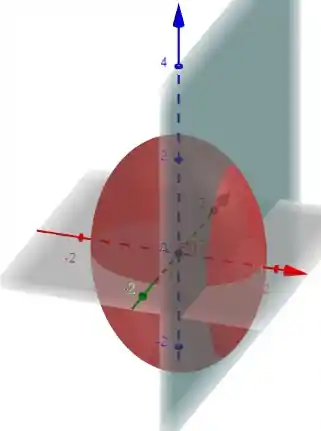
E observar a curva da interseção das duas superfícies, plano e elipsoide. Algebricamente podemos fazer um sistema
E olha que maravilha, conseguimos nossa curva, uma elipse!
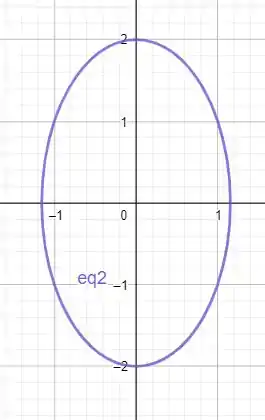
Terminamos por aqui. Te vejo na próxima resolução
: )