Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.6 - Ex. 5
Escreva uma equação polar de uma cônica com o foco na origem e com os dados fornecidos.
Passo 1
Beleza, pessoal? Vamos escrever uma equação polar pra essa parábola, você lembra como é a fórmula? Bom, existem algumas possibilidades, né mesmo?
Então, qual usar? Pra poder escolher, a gente precisa de mais algumas informações sobre a reta diretriz, né? Mas o enunciado só nos deu o vértice, que chato!
Passo 2
Porém, podemos usar o fato de que o vértice de uma parábola fica a meio caminho entre o foco e a reta diretriz, certo? Vamos primeiro passar as coordenadas polares do vértice para coordenadas retangulares, ok?
Então, nosso vértice está no ponto . Como o foco está na origem , só nos resta dizer que a reta diretriz é . Veja o desenho a seguir pra visualizar isso melhor:
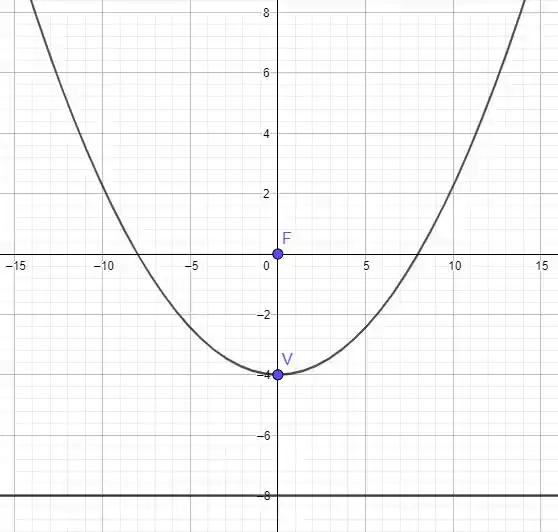
Passo 3
Show! Agora que a gente sabe que a reta diretriz é paralela ao eixo e está abaixo desse eixo, podemos escrever a fórmula:
Como estamos falando de parábola, já sabemos que . E como a reta diretriz tem equação , então .