Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.6 - Ex. 6
Escreva uma equação polar de uma cônica com o foco na origem e com os dados fornecidos.
Passo 1
Beleza, galera? Bora achar uma equação polar pra essa elipse?
A gente precisa escrever uma equação na forma polar, de uma curva cônica, que nesse caso é a elipse, com uma excentricidade de e vértice de .
As possíveis fórmulas cônicas para elipses são essas:
Onde é a excentricidade. Se a gente tem uma cônica. E é a diretriz.
As figuras abaixo nos ajudam a escolher qual equação a gente utiliza em determinada situação:
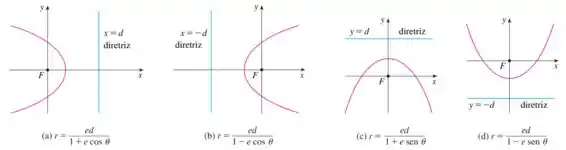
Se soubéssemos a equação da reta diretriz, poderíamos determinar qual dessas fórmulas usar. Mas, não sabemos, só temos a excentricidade, o vértice e o foco (na origem).
Uma informação que ele nos deu foi a localização do vértice, mas em coordenadas polares. Vamos passar pra coordenadas retangulares:
Então temos a nova informação de que um dos vértices está no ponto , mas como usaremos isso?
Passo 2
Repare que tanto um dos focos como um dos vértices estão no eixo , o que significa que o eixo maior da elipse é vertical.
Quando isso acontece, nós usamos a fórmula com , e é interessante que você guarde isso na memória.
Talvez o esqueminha a seguir te ajude a guardar isso:
Elipse com eixo maior vertical temos que o eixo :
Utilizamos a fórmula com o seno.
Já a elipse com o eixo maior na horizontal temos que o eixo :
Utilizamos então a fórmula com o cosseno.
Voltando ao nosso caso, nossa equação vai ser do tipo:
Como temos as coordenadas polares do vértice, podemos substituir esses valores pra encontrar o valor de , já que sabemos que , beleza?
Temos então que:
Então o nosso :
Passo 3
Você pode estar achando estranho termos chegado a dois resultados diferentes para , né?
Mas nesse caso, é bem razoável, pois apenas um foco e um vértice não determinam completamente uma elipse, precisaríamos de mais um vértice ou mais um foco para tal.
Então as possíveis equações ficarão assim, substituindo seus respectivos valores de :
Show?