Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.5 - Ex. 21
Calcule a integral.
Passo 1
Aqui como temos que o coeficiente de no numerador é maior que o do denominador vamos dividir os dois:
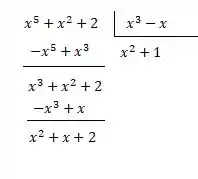
Temos então que:
Temos então que a integral fica:
Agora vamos resolver as três integrais separadamente.
Passo 2
Com a primeira, para achar as primitivas da função, vamos usar essa expressão da Tabela de Integrais Indefinidas:
Aplicando:
Passo 3
Com a segunda, para achar as primitivas da função, vamos usar essa expressão da Tabela de Integrais Indefinidas:
Aplicando:
Passo 4
Com a terceira vamos analisar o denominador, ele pode ser decomposto em:
Ele então é um produto de fatores lineares distintos, vamos então usar a seguinte fórmula:
Vamos achar os valores de , e , vamos multiplicar os lados da equação pelo produto dos denominadores :
Vamos destrinchar essa expressão agora e isolar os termos do polinômio:
Passo 5
Temos uma igualdade de polinômios, então valos igualar os coeficientes de de cada lado, e os termos constantes também, assim vamos ficar com o sistema:
Temos que o valor de é:
Substituindo na primeira:
Isolando na segunda:
Substituindo na primeira temos:
Temos então que :
Pronto, achamos os valores de , e , vamos agora substituir de volta na integral:
Agora vamos resolver as três integrais separadamente.
Passo 6
Com a primeira para achar as primitivas da função, vamos usar essa expressão da Tabela de Integrais Indefinidas:
Aplicando:
Passo 7
Com a segunda, vamos usar a Regra da Substituição:
Vamos agora achar diferencial de , derivando:
Fazendo a substituição ficamos com:
Aqui, para achar as primitivas da função, vamos usar essa expressão da Tabela de Integrais Indefinidas:
Aplicando:
Passo 8
Vamos usar a Regra da Substituição novamente agora na terceira:
Vamos agora achar diferencial de , derivando:
Fazendo a substituição ficamos com:
Aqui, para achar as primitivas da função, vamos usar essa expressão da Tabela de Integrais Indefinidas:
Aplicando:
Passo 9
Agora é só juntar tudo:
Calma, não terminou ainda, não esqueça de voltar para a variável , é só substituir de volta o que você usou no começo: