Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 7.4 - Ex. 6
Escreva as formas de decomposição em frações parcias da função (como no Exemplo ). Não determine os valores numéricos dos coeficientes.
Passo 1
Fala aí! como vai?
Nesse problema temos duas frações e nosso objetivo é reescrever essas frações em frações parciais.
Lembra como fazemos isso?
A ideia de decompor uma função em frações parciais é que dessa forma podemos transformar uma função relativamente complexa em somas de funções mais simples.
Veja só!
Passo 2
- Nosso primeiro passo é fatorar o denominador, vamos isolar o menor termo de , que é o e achar as raízes do outro polinômio:
- Nosso primeiro passo é fatorar o denominador, vamos isolar o menor termo de , que é o :
Agora vamos fatorar o denominador, achando as raízes de temos:
Usando Bhaskara:
Poxa, achamos o delta negativo, então não teremos raízes reais.
Aqui temos o Caso I o Caso III, onde o denominador é um produto de fatores lineares distintos, e onde contém fatores quadráticos irredutíveis sem repetição:
Tranquilo até aqui?
Passo 3
Agora da pra ver que é raiz de , então vamos dividir ele por :
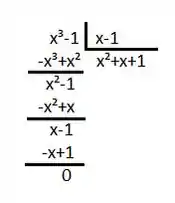
Assim ficamos com:
Aqui temos o Caso I, Caso II e o Caso III, onde o denominador é um produto de fatores lineares distintos, que se repetem, e onde contém fatores quadráticos irredutíveis sem repetição, vamos usar a fórmula então:
E aí! entendeu tudo? Responde Aí!