Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 33

Escreva uma fórmula por partes para a função:

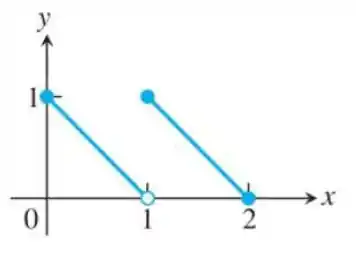
Passo 1

Olá! Vamos achar uma equação pra primeira reta, uma pra segunda e aí vamos colocar tudo como uma função só, ok?

Passo 2

Para achar a equação da primeira reta:

Vamos jogar os pontos que tem ali (0,1) e (1,0) na equação geral da reta:

y = a x + b -> 1 = a * 0 + b -> b = 1

y = a x + b -> 0 = a * 1 + b -> a + b = 0 -> a + 1 = 0 -> a = - 1

y = a x + b -> y = - x + 1

Passo 3

Para achar a equação da segunda reta:

Vamos jogar os pontos que tem ali (1,1) e (2,0) na equação geral da reta:

y = a x + b -> 1 = a * 1 + b -> a + b = 1 -> b = 1 - a

y = a x + b -> 0 = a * 2 + b -> 2 a + b = 0 -> 2 a + 1 - a = 0 -> a + 1 = 0 -> a = - 1

b = 1 - a -> b = 1 - ( - 1 ) -> b = 2

y = a x + b -> y = - x + 2

Resposta

y = { - x + 1 , se 0 <= x < 1 e - x + 2 , se 1 <= x <= 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se f (x) = x - 1 e g (x) = 1 // ( x + 1 ) , resolva:f (g (1 // 2)) g (f (1 // 2)) f (g (x)) g (f (x)) f (f (2)) g (g (2)) f (f (x)) g (g (x))
Se f (x) = x + 5 e g (x) = x^2 - 3 , resolva:f (g (0)) g (f (0)) f (g (x)) g (f (x)) f (f (- 5)) g (g (2)) f (f (x)) g (g (x))
Se f x = x - 1 e g x = 1 / ( x + 1 ) , resolva: f g 1 / 2 g f 1 / 2 f g x g f x f f 2 g g 2 f f x g g x
Se f (x) = x + 5 e g (x) = x^2 - 3 , resolva:f (g (0)) g (f (0)) f (g (x)) g (f (x)) f (f (- 5)) g (g (2)) f (f (x)) g (g (x))
Se f (x) = x - 1 e g (x) = 1 // ( x + 1 ) , resolva:f (g (1 // 2)) g (f (1 // 2)) f (g (x)) g (f (x)) f (f (2)) g (g (2)) f (f (x)) g (g (x))