Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.2 - Ex. 1
Escreva, mas não calcule, uma integral para a área da superfície obtida pela rotação da curva em torno do (a) eixo x e (b) eixo y.
,
Passo 1
Eaeee, belezinha??? Bom... o enunciado nos dá a seguinte função:
No intervalo .
Bom... essa é uma questão introdutória sobre áreas de superfície de revolução.
Queremos encontrar a integral para a área da superfície obtida pela rotação da curva em torno do eixo e eixo .
Mas a gente não precisa calcular a integral, viu?
Para isso, é sempre bom fazer um esboço da curva né?
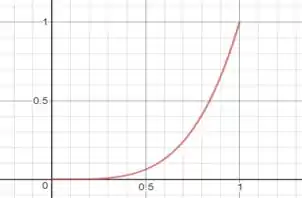
Agora vamos rotacionar em torno dos eixos e ver o que acontece 😉
Passo 2
Rotacionando em torno do eixo , a integral é calculada na variável e é dada por
Assim, como , temos que .
Desta forma, temos que:
Em consequência disso, ao substituir na fórmula, ficamos com:
Passo 3
Para a rotação em torno do eixo , a integral é dada por
onde é dado como função de .
Assim, para , o trecho da curva considerado pode ser dado .
Portanto:
Além disso, note que os limites de integração na variável também vão de até .
Desta forma,
Resposta
a)
b)