a) Escreva e usa a regra da cadeia para mostrar que
b) Se , encontre e esboce os gráficos de e . Onde não é derivável?
c) Se , encontre e esboce os gráficos de e . Onde não é derivável?
Passo 1
Eaee, belezinha??? Bom.. essa é uma questão bem direta ao ponto haha.
Essa é uma questão que trabalha com a diferenciabilidade da função módulo.
Sabemos que a função modular é derivável em toda parte exceto em onde apresenta um bico.
No item (a), devemos mostrar uma relação para a derivada do módulo e nos itens (b) e (c) devemos usar essa relação com funções compostas para identificar os pontos em que as funções e não são deriváveis.
Para resolver essa questão podemos apenas pegar a definição da regra da cadeia, onde temos que se:
Então:
Agora bora lá!! 😉
Passo 2
Vamos usar a regra da cadeia para resolver o item (a).
Antes disso: . Assim, pela regra da cadeia:
Note que a expressão não está definida para : de fato, a função modular não é derivável na origem.
Passo 3
Da regra de composta de funções, a função será derivável em todos os pontos exceto nos pontos que zerem o módulo.
Isso ocorre para , logo, para , com inteiro.
Assim, é derivável em todos os pontos exceto nos pontos do tipo , com .
Agora vamos usar que de modo que .
Assim, pela regra da cadeia:
Passo 4
O gráfico de é :
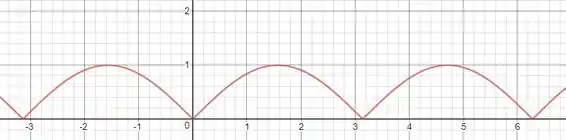
Note que a função é periódica e, elém disso, tem bicos em pontos igualmente espaçados (e cujo espaçamento é ).
Passo 5
O gráfico de é:
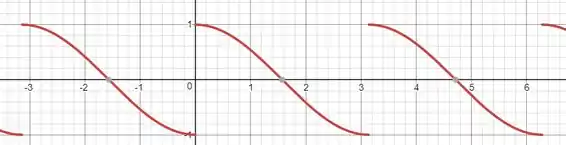
Observe que as descontinuidades de ocorrem exatamente nos pontos em que não é derivável.
Passo 6
Agora temos de modo que .
Assim, o único valor que pode anular o módulo é e, portanto, é derivável em .
Pela regra da cadeia:
Passo 7
O gráfico de é:

Note que o único bico ocorre em .
E o gráfico de é:

Resposta
a) Demonstração.
b)
c)