Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.5 - Ex. 17f

Escrever na forma de uma integral tripla iterada:

∫ ∫ ∫ T f d V

Onde T é a região interior ao cilindro x 2 - x + y 2 = 0   e   à   x 2 + y 2 + z 2 = 1

Passo 1

Lembra que na integral tripla o d V   é a mesma coisa que d x d y d z , então sabemos que as integrais triplas podem ser calculadas de forma análoga às integrais duplas, por meio de integrações sucessivas.

Para calcular as integrais duplas precisávamos ter noção da região de integração, aqui em integrais triplas vamos precisar da mesma noção e isso é justamente iterar a nossa integral tripla.

Passo 2

Precisamos analisar a delimitação da nossa superfície T

Estamos tratando da seguinte região:

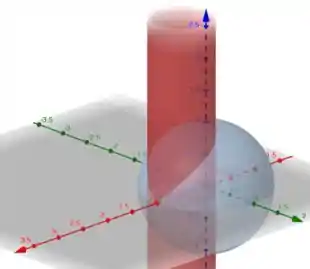
Nossa região é a intersecção entre um cilindro deslocado da origem e uma esfera

A equação do cilindro é : x - 1 2 2 + y 2 = 1 4

Portanto, o limite da região será dado por:

0 ≤ x ≤ 1

- 1 4 - x - 1 2 2 ≤ y ≤ 1 4 - x - 1 2 2

- ( 1 - x 2 - y 2 ) ≤ z ≤ ( 1 - x 2 - y 2 )

Passo 3

Agora vamos deixar nossa integral na forma com as três variáveis e depois colocá-la na forma iterada :

∫ ∫ ∫ T f d V =   ∫ 0 1 ∫ - 1 4 - x - 1 2 2 1 4 - x - 1 2 2 ∫ - ( 1 - x 2 - y 2 ) ( 1 - x 2 - y 2 ) f d z d y d x

Resposta

∫ 0 1 ∫ - 1 4 - x - 1 2 2 1 4 - x - 1 2 2 ∫ - ( 1 - x 2 - y 2 ) ( 1 - x 2 - y 2 ) f d z d y d x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

∭ E z x 2 + z 2 d V , onde E = { ( x , y , z ) | 1 ≤ y ≤ 4 ,y ≤ z ≤ 4 ,0 ≤ x ≤ z }
Calcule a integral iterada. ∫ 1 2 ∫ 0 2 z ∫ 0 ln ⁡ x x e - y d y d x d z
Calcule a integral iterada. ∫ 0 2 ∫ 0 z 2 ∫ 0 y - z 2 x - y d x d y d z
Calcule a integral iterada. ∫ 0 1 ∫ 0 1 ∫ 0 1 - z 2 z y + 1 d x d z d y
Calcule a integral tripla. ∭ E e z / y d V Onde, E = x , y , z | 0 ≤ y ≤ 1 , y ≤ x ≤ 1,0 ≤ z ≤ x y