Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 3.2 - Ex. 34
Quando o esquecimento é levado em conta,a taxa de memorização de uma pessoa é dada por:
Em que , . é a quantidade de material memorizada no instante , é a quantidade total a ser memorizada e é a quantidade restante a ser memorizada. Encontre e esboce um gráfico da solução. Suponha . Calcule o valor limite de quando e interprete o resultado.
Passo 1
Então galera, o objetivo dessa questão é, basicamente, resolvermos a equação diferencial que nos foi dado, tudo bem? A equação é a seguinte:
Reescrevendo essa equação, teremos:
O formato dessa equação é:
No qual e são funções APENAS de . Esse tipo de equação tem uma solução geral padrão, que é:
Sendo assim, o que precisamos fazer é definir quem é e quem é e depois resolver essas integrais. Então mãos a obra!
Passo 2
Da nossa equação tiramos que:
Passo 3
Sustituindo o que encontramos na nossa solução, teremos:
Resolvendo a integral do expoente:
Substituindo na solução:
Agora resolvendo a integral de dentro:
Substituindo, teremos:
Simplificando:
Show!
Passo 4
A princípio resolvemos nossa equação diferencial, no entanto a questão nos dá uma condição inicial para determinarmos . Aplicando a condição , teremos:
Substituindo na solução:
E esse é nosso resultado final!
Passo 5
O enunciado ainda nos pede duas coisas antes de finalizar a questão: que plotemos o gráfico da função e que façamos uma análise para . Então bora que bora!
Para teremos o seguinte resultado:
O resultado nos mostra que nunca conseguiremos memorizar completamente o conteúdo estudado. O gráfico da nossa função é o seguinte:
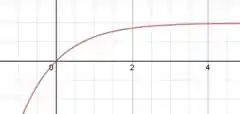
E está aí nossa resposta, galeris! 😉
Resposta
Para :