Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.2 - Ex. 27

Estabeleça as equações paramétricas para a reta tangente a curva dada pelas equações paramétricas, no ponto especificado. Ilustre traçando o gráfico da curva e da reta tangente em uma mesma tela.

x = t ,   y = 2 cos ⁡ t ,   z = 2 s e n   t           ( π / 4,1 , 1 )

Passo 1

Fala ai gelerinha. De boa? Bora resolver essa questão?

Nosso objetivo é encontrar as equações paramétricas da reta tangente a uma curva dada pelas suas equações paramétricas x = t ,     y = 2 cos ⁡ t ,     z = 2 s e n   t em um ponto específico   π 4 , 1,1 . Além disso, precisamos ilustrar graficamente tanto a curva quanto a reta tangente.

Vamos seguir os passos:

  1. Primeiro temos que determinar o vetor tangente. Para isso iremos derivar as funções x ( t ) , y ( t ) e z ( t ) em relação a t para obtermos as componentes do vetor tangente.e
  2. E avaliarmos as derivadas no ponto específico.
  3. A equações paramétricas serão encontradas usando o ponto e o vetor da reta tangente. Substituindo em:

    4. x = x 0 + a t

    y = y 0 + b t

    z = z 0 + c t

    Onde ( x 0 , y 0 , z 0 ) é o ponto na curva e ( a , b , c ) são as componentes do vetor tagente.

  4. E por último, temos que utilizar uma ferramente de visualização gráfica para plotar o gráfico.

Vamos começar a resolver. E só seguir os passos!

Passo 2

Vamos encontrar o vetor tangente.

Para d x

d x d t = d d t t

d x = 1

Para d y

d y d t = d d y 2 cos ⁡ t

O termos 2 é constante.

d y = 2 d d y cos ⁡ t

d y = - 2 s e n   t

Para d z

d z d t = d d t 2 s e n   t

O termos 2 é constante.

d z = 2 d d t s e n   t

d z = 2 cos ⁡ t

Passo 3

Substituindo t = π 4 , obtermos o vetor tangente.

Para x

d x = 1

Para y

d y = - 2 s e n   t

d y = - 2 ∙ s e n   π 4

d y = - 2 ∙ 2 2

d y = - 4 2 = - 2 2 = - 1

Para z

d z = 2 cos ⁡ t

d z = 2 cos ⁡ π 4

d z = 2 ∙ 2 2

d z = 4 2 = 2 2 = 1

O ponto tangente é 1 , - 1,1

Passo 4

Agora vamos substituir os termos nas equação paramétricas

x = x 0 + a t

y = y 0 + b t

z = z 0 + c t

Onde ( x 0 , y 0 , z 0 ) é o ponto π 4 , 1,1 e ( a , b , c ) é 1 , - 1,1 . Temos então

x = π 4 + t

y = 1 - t

z = 1 + t

Passo 5

Utilizando um programa de visialização gráfica, obtemos a curva com a reta tangente:

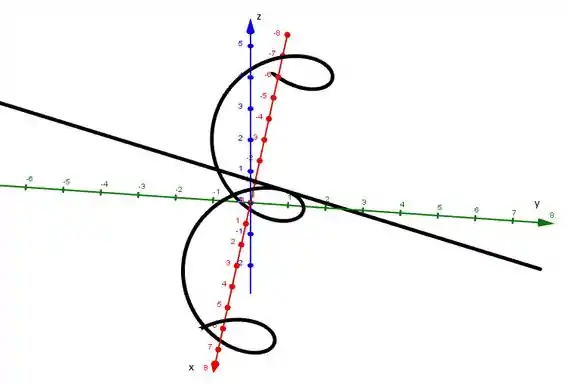
Resposta

A equação paramétrica da reta tangente é:

x = π 4 + t

y = 1 - t

z = 1 + t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre uma equação vetorial e equações paramétricas para o segmento de linha que une P e Q : P - 1,2 , - 2 Q ( - 3,5 , 1 )
Esboce a curva com a equação vetorial fornecida. Indique uma seta, o sentido na qual t aumenta: r t =3 , t , 2 - t 2
Encontre uma equação vetorial e equações paramétricas para o segmento de linha que une P e Q : P 2,0 , 0 Q ( 6,2 , - 2 )
Encontre o comprimento da curva para 4 casas decimais. (Use uma calculadora para aproximar a integral.) r → t = t 2 , t 3 , t 4 0 ≤ t ≤ 2
(a) Encontre a função de comprimento de arco para a curva medida a partir do ponto P na direção de aumento de t, em seguida reparametrize a curva em realação ao comprimento de arco para o ponto P, e (