Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.2 - Ex. 28
Estabeleça as equações paramétricas para a reta tangente a curva dada pelas equações paramétricas, no ponto especificado. Ilustre traçando o gráfico da curva e da reta tangente em uma mesma tela.
Passo 1
Olá, meu querido amigo. Vou te ajudar a resolver essa atividade.
Para encontrarmos a equação paramétrica da reta tangente precisamos primeiramente saber quem é nossa equação vetorial. Neste caso é:
Desta forma a equação paramétrica da reta tangente é dada por um ponto e por um vetor pertencente a essa reta.
Precisamos então do vetor diretor:
No ponto de tangencia, e o ponto de tangencia:
O ponto pertencente a essa reta já é dado:
Já o vetor nos precisamos encontrar e ele é dado pela derivada da equação vetorial da superfície.
Passo 2
Desta forma a derivada de uma equação vetorial é a derivada de cada componente.
Derivada da componente :
Derivada da componente :
Derivada da componente :
Portanto é:
Passo 3
O ponto dado pertencente a reta tangente corresponde ao parâmetro , aplicando em temos:
Desta forma a equação paramétrica da reta tangente é:
Substituindo o que encontramos:
Passo 4
O gráfico da curva com a reta tangente é encontrado utilizando o GeoGebra 3D, para melhor visualização nossa:
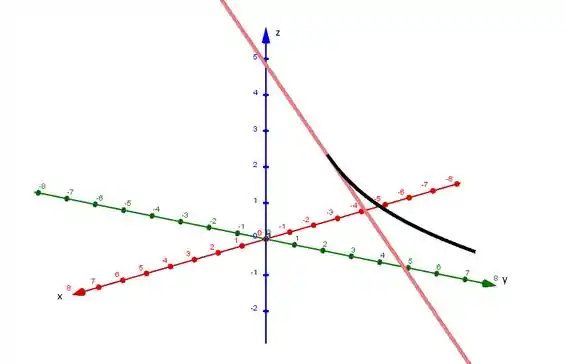
Resposta
A equação paramétrica da reta tangente é: