Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.5 - Ex. 9
9. Um estacionamento para estudantes em uma universidade cobra $2,00 para a primeira meia hora (ou para qualquer fração) e $1,00 para cada meia hora subsequente (ou para qualquer fração) até uma diária máxima de $10,00.
(a) Esboce o gráfico do custo como função do tempo de estacionamento.
(b) Discuta o significado da descontinuidade no gráfico para um estudante que utiliza o estacionamento.
Passo 1
(a) Considerando o eixo horizontal como tempo dado em horas e o eixo vertical como os valores em função do tempo, que são dados em reais, vamos construir o gráfico usando a definição da função descrita no enunciado, isto é:
De , o custo é de , e esse valor é assumido em todo o intervalo. Como a cada meia hora se soma , desta forma temos que de , o custo é de , e assim por diante em intervalos da forma com O gráfico gerado é da forma:
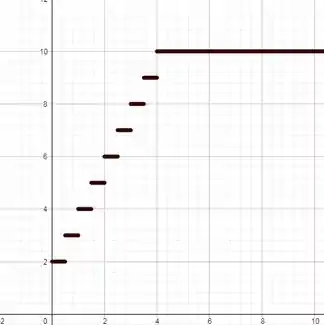
Passo 2
(b) A descontinuidade no gráfico se dá pelos saltos entre os valores para cada meia hora que se passa, segundo a lei que define os custos do estacionamento. Esses saltos ocorrem porque no instante em que se completa meia hora, a próxima meia hora já começa a ser contada, portanto adiciona o valor ao custo total, ou seja, o valor não é adicionado ao longo do tempo, mas é adicionado em um determinado instante de tempo.
Resposta
Gráfico e análise acima.