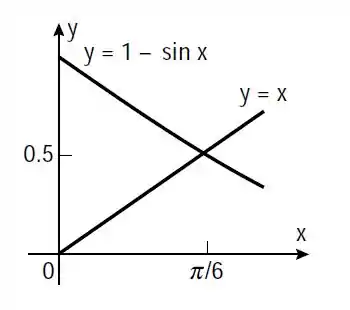Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.6 - Ex. 68

  1. Use o Teorema do Valor Intermediário para mostrar que a equação x + sen ⁡ x = 1 tem pelo menos uma solução no intervalo 0 , π 6 .
  2. Mostre graficamente que existe exatamente uma solução no intervalo.
  3. Aproxime a solução com três casas decimais de precisão.

Passo 1

  1. Primeiro vamos fazer:

    2. g x = x + s en ⁡ x - 1

    Agora vamos achar os valores de g 0 e g π 6 :

    g 0 = x + sen ⁡ x - 1 = 0 + sen ⁡ 0 - 1 = - 1

    g π 6 = x + sen ⁡ x - 1 = π 6 + sen ⁡ π 6 - 1 = π 6 + 1 2 - 1 = π 6 - 1 2

    Assim, temos que como g x é uma função contínua, pelo Teorema do Valor Médio, existe um valor c entre 0 e π 6 onde g c = 0 , o que implica que existe um c no intervalo 0 , π 6 .

    Passo 2

  2. Vamos plotar as duas equações:

    3. y = x e y = 1 - s en ⁡ x

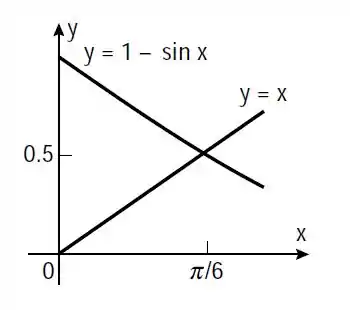
    Pronto, dá pra ver pelo gráfico que as duas curvas se interceptam em apenas um ponto.

    Passo 3

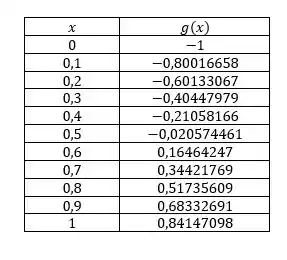
  3. Pelo gráfico sabemos que a raiz está entre 0 e 1 , vamos então dividir o intervalo em 10 intervalors iguais e avaliar g nos pontos finais:

O valor de g x muda de sinal de 0 , 5 para 0 , 6 , e pelo Teorema do Valor Médio, existe um c no intervalo 0 . 5 , 0 . 6 tal que g c = 0 .

Agora vamos dividir esse novo intervalo em 10 partes iguais feito o que acabamos de fazer:

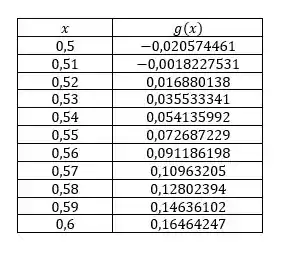
Agora g x muda de sinal de 0 , 51 para 0 , 52 , e pelo Teorema do Valor Médio, existe um c no intervalo 0 . 51 , 0 . 52 tal que g c = 0 .

Vamos dividir esse novo intervalo em 10 partes iguais:

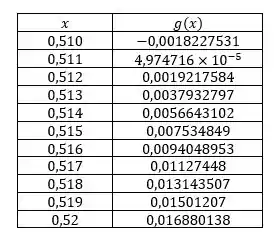
Aqui g x muda de sinal de 0 , 510 para 0 , 511 , e pelo Teorema do Valor Médio, existe um c no intervalo 0 . 510 , 0 . 511 tal que g c = 0 .

Para achar o valor aproximado vamos tirar a média dos valores do intervalo:

0 , 510 + 0 , 511 2 = 0 , 51 0

Resposta

  2. 0 , 510
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

56-Suponha que f seja contínua no intervalo [ 0,1 ] e que 0 ≤ f ( x ) ≤ 1 para todo x nesse intervalo.a)Esboce o gráfico de y = x junto a um gráfico possível de f sobre o intervalo [ 0,1 ] .b)Use o Te
1-4 Seja a função f a função cujo gráfico é dado. Em quais (se houver) dos intervalos seguintes f é contínua ?a) [ 1,3 ] b) ( 1,3 ) c) [ 1,2 ] d) ( 1,2 ) e) [ 2,3 ] f) ( 2,3 )
5- Considere as funções: f x = 1 ,x ≠ 4 - 1 ,x = 4e g ( x ) 4 x - 10 ,x ≠ 4 - 6 ,x = 4 Em cada parte verifique se a função dada é contínua em x = 0 a) f x b) g ( x ) c ) - g ( x ) d) f ( x ) e) f x .
38. a) Use um recurso computacional para gerar o gráfico da função f( x )=x x 3 - x + 2 e, então, use o gráfico para fazer uma conjectura sobre o número e a localização de todas as descontinuidades.b)
6. Considere as funções: f x = 1 ,0 ≤ x 0 ,x0e g ( x ) 0 ,0 ≤ x 1 ,x0 Em cada parte verifique se a função dada é contínua em x = 0 a) f x b) g ( x ) c ) f ( - x ) d) g ( x ) e) f x . g ( x ) f) f ( g