Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.4 - Ex. 39
39. Estenda primeiro a de modo que seja simétrica em relação à reta . Então satisfaz para . Estenda a função resultante a como ímpar e ao resto da reta real como periódica de período (veja a Figura 10.4.7). Mostre que essa função tem série de Fourier formada pelas funções , , , . . . ; ou seja,
em que
Essa série converge para a função original em .
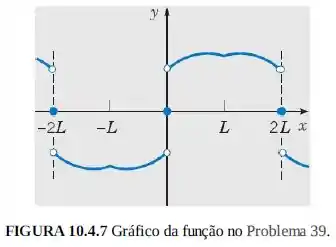
Passo 1
Fala galera!!
Vamos considerar o gráfico da função no intervalo em que se estendeu o gráfico da função para em que o gráfico seja simétrico em relação à linha. Então satisfaz a equação para . Agora, fazemos uma extensão impar para de modo que , .
Assim, temos que o gráfico da função é representado da seguinte maneira:
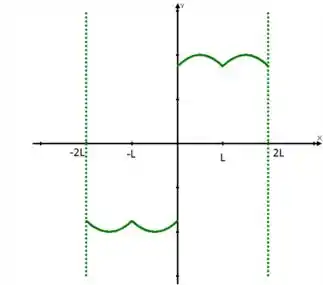
Passo 2
Para uma função ímpar no intervalo de , a série de funções de Fourier é uma série senoidal dada pela seguinte expressão:
Em que é dado pela seguinte expressão:
Podemos abrir a integral da seguinte maneira:
Na primeira integral, podemos fazer a seguinte substituição:
Quando temos que e quando temos que .
Assim temos:
Mas, no intervalo de , temos que . Substituindo, temos:
Passo 3
Para o caso em que é par, temos que . Assim temos:
Para o caso em que é ímpar, temos que . Assim temos:
Podemos fazer a substituição
Quando temos que e quando temos que .
Mas, no intervalo de , temos que . Substituindo, temos:
Para o caso em que é ímpar, temos que . Assim temos:
Como estamos considerando só quando é impar, podemos reescrever da seguinte maneira:
Assim temos que a série de Fourier é a seguinte:
Em que
Resposta
Ei, a resposta está no passo a passo :)