Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.4 - Ex. 12

Em cada um dos problemas de 7 a 12, é dada uma função f em um intervalo de comprimento L . Em cada caso, esboce os gráficos da extensão par e da extensão ímpar de f de período 2 L .

12.

f x = 4 - x 2   ,             0 < x < 1

Passo 1

Fala galera!!

Nos foi dado a seguinte função:

f x = 4 - x 2   ,             0 < x < 1

Queremos esboçar os gráficos de uma extensão impar e de uma extensão par da função f ( x ) . Temos que Uma função f é considerada par quando  f - x = f x , qualquer que seja o valor de x   Є   D f . Temos também que uma função f é considerada ímpar quando  f - x = - f x , qualquer que seja o valor de x   Є   D f .

Passo 2

A função dada é definida para um período L de intervalo ( 0 ,   1 ) . Para a extensão par desta função, podemos definir uma função g x do período 2 L de intervalo ( - 1 ,   1 ) tal que:

g x = f - x , f x ,             - 1 ≤ x < 0 0 ≤ x ≤ 1

Ou seja, para a função f x = 4 - x 2   , temos que:

f - x = 4 - - x 2

= 4 - x 2

Reescrevendo como uma função g x temos:

g x = 4 - x 2 - 1 ≤ x < 0 4 - x 2       0 ≤ x ≤ 1

Ou

g x = 4 - x 2   - 1 ≤ x ≤ 1

Agora, podemos plotar o gráfico de 3 períodos da função g x que representa a extensão par da função f x . Assim temos:

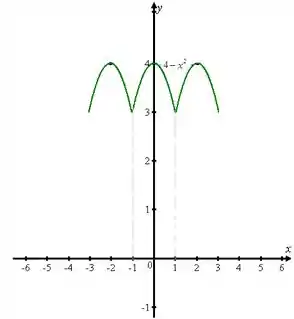
Passo 3

A função dada é definida para um período L de intervalo ( 0 ,   1 ) . Com em uma função impar

f - x = - f x

Ou

f x = - f - x

Assim, para uma extensão impar desta função, podemos definir uma função h x do período 2 L de intervalo ( - 1 ,   1 ) tal que:

h x = - f - x , f x ,             - 1 ≤ x < 0 0 ≤ x ≤ 1

Ou seja, para a função f x = 4 - x 2   , temos que:

- f - x = - 4 - - x 2  

= x 2 - 4

Reescrevendo como uma função h x temos:

h x = x 2 - 4 - 1 ≤ x < 0 4 - x 2       0 ≤ x ≤ 1

Agora, podemos plotar o gráfico de 3 períodos da função h x que representa a extensão impar da função f x . Assim temos:

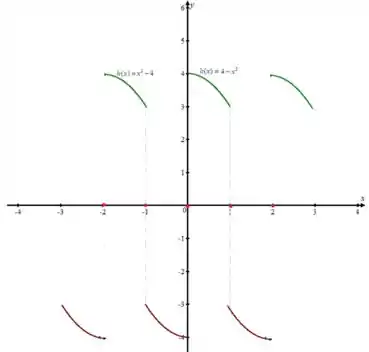
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13. Prove que qualquer função pode ser expressa como a soma de uma função par com uma função ímpar. Ou seja, para qualquer função f cujo domínio contém - x sempre que contiver x , mostre que há uma fu
Em cada um dos problemas de 7 a 12, é dada uma função f em um intervalo de comprimento L . Em cada caso, esboce os gráficos da extensão par e da extensão ímpar de f de período 2 L .11. f x = 0 , 1 , 0
Em cada um dos problemas de 15 a 22:(a) Encontre a série de Fourier indicada para a função dada.(b) Esboce o gráfico da função para a qual a série converge em um intervalo de três períodos.20. f x = x
14. Encontre os coeficientes para as séries em cossenos e em senos descritas no Exemplo 2.
Em cada um dos problemas de 7 a 12, é dada uma função f em um intervalo de comprimento L . Em cada caso, esboce os gráficos da extensão par e da extensão ímpar de f de período 2 L .8. f x = 0 , x - 1