Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.1 - Ex. 16
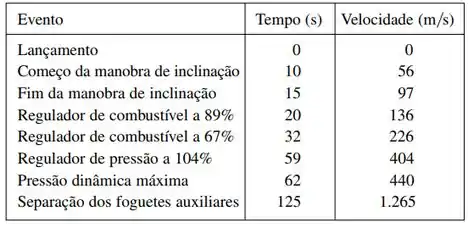
Quando estimamos distâncias a partir dos dados da velocidade, algumas vezes é necessário usar tempos que não estão igualmente espaçados. Podemos ainda estimar as distâncias usando os períodos de tempo . Por exemplo, em 7 de maio de 1992, o ônibus espacial Endeavour foi lançado na missão STS-49, cujo propósito era instalar o satélite de comunicação Intelsat. A tabela, fornecida pela Nasa, mostra os dados da velocidade do ônibus entre o lançamento e a entrada em funcionamento dos foguetes auxiliares. Use estes dados para estimar a altura acima da superfície da Terra do segundos depois do lançamento.
Passo 1
Opa! Bora pra mais uma questão? O enunciado nos dá uma tabela com dados de velocidade do ônibus espacial Endeavour após seu lançamento da terra em 7 de maio de 1992:
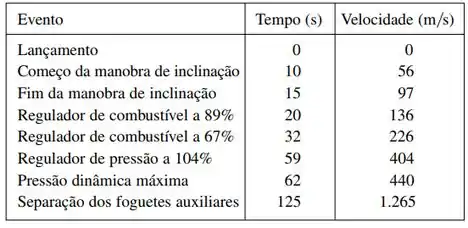
E pede pra a gente usar estes dados para estimar a altura acima da superfície da Terra do segundos após o lançamento.
Como nossos intervalos não são igualmente espaçados, para calcular a altura faremos:
Onde e são as velocidades e o intervalo de tempo no intervalo e é o número de intervalos.
Nesse caso como queremos para usaremos intervalos.
Agora bora lá!! 😉
Passo 2
Assim, a distância viajada após segundos pode ser aproximada por:
Olhando a tabela, vamos substituir dessa forma:
Que será a velocidade x , e faremos isso sucessivamente, até termos 6 membros nessa equação.
Desta forma:
Calculando:
Prontinho! 😉
