Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.4 - Ex. 23
É mostrado o gráfico da concentração depois da injeção de de contraste em um coração. Use a Regra de Simpson para estimar a capacidade cardíaca.
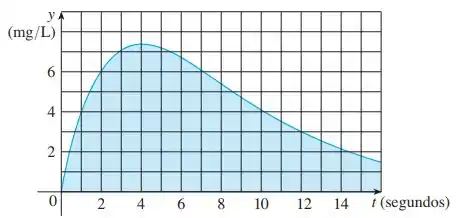
Passo 1
Pra estimar a pressão de saída do coração, assim como no exemplo 2, nós vamos usar a Regra de Simpson’s com .
Passo 2
Passo 3
Portanto,
Resposta
R:
Exercícios de Livros Relacionados
O gráfico de g é apesentado. Estime ∫ 2 4 g x d x com seis subintervalos usando Pontos médios
Se f x = x 2 - 2 x ,0 ≤ x ≤ 3 , calcule a soma de Rieman com n = 6 correta até a 6 casa decimal, tomando como pontos amostrais da direita. O que representa a soma de Rieman? Ilustre com um diagrama.
Use a forma da definição de integral dada no Teorema 4 para calcular a integral. ∫ 0 1 x 3 - 3 x 2d x
Use a forma da definição de integral dada no Teorema 4 para calcular a integral. ∫ - 2 0 x 2 + xd x
Use a forma da definição de integral dada no Teorema 4 para calcular a integral. ∫ 0 2 2 x - x 3