Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.1 - Ex. 1
Dê uma estimativa para a área entre o gráfico da função e o intervalo Use um esquema de aproximação com retângulos, análogo ao desenvolvido nesta seção para a função . Se seu recurso computacional efetuar somatórios automaticamente, estime a área especificada usando e retângulos. Caso contrário, estime a área usando retângulos.
Passo 1
Já que vamos usar o método dos retângulos para calcular a área, vamos começar subdividindo o intervalo em subintervalos iguais, cada um, portanto, com comprimento de ; as extremidades dos subintervalos ocorrem em:
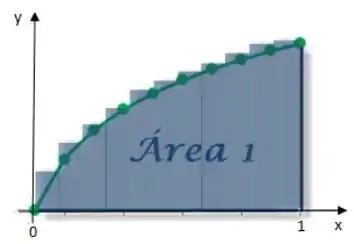
Passo 2
A área do triângulo é , sendo que a base de todos eles vai ser pois dividimos o intervalo de tamanho em pedacinhos. E a altura vai ser exatamente o naquele ponto, ou seja, dado que as alturas serão:
Como todas as bases dos retângulos são iguais, temos então que a área total é:
Então:
Passo 3
Para :
Para :
Para :
Para
Para :
Resposta
