Dê uma estimativa para o valor de (), tal que a região englobada por , e tenha uma área de unidade.

Vamos usar um recurso gráfico para esboçar nossa região. Como , sabemos que está depois de .

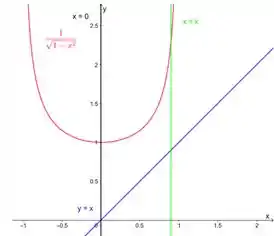
A gente percebe que como temos funções que variam em , é melhor montarmos a integral em relação a esse eixo. Outra coisa que vemos é que nossa região é limitada por cima pela função (função maior) e por baixo pela função (função menor). Aí integral fica com essa carinha:

Pelo gráfico já dá para ver que nossos extremos de integração são e

Nossa integral fica:

A gente sabe pelo enunciado que , então:

Agora vamos calcular essa integral aí. Fica:

Agora usamos um programa para resolver a equação: