Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 7.7 - Ex. 29
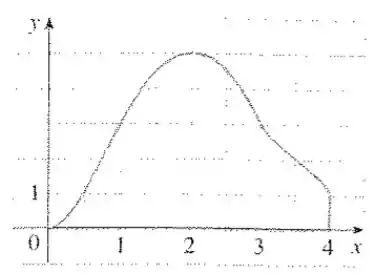
Estime a área sob o gráfico na figura usando a Regra do Trapézio, a Regra do Ponto Médio e a Regra de Simpson, cada qual com .
Passo 1
Para estimar a área do gráfico usando cada um dos métodos basta utilizarmos as fórmulas presentes no livro e utilizar as especificações dadas no enunciado/gráfico. Assim, temos que
Para a regra do trapézio vamos ter
Agora pela regra do ponto médio vamos obter
Por fim, utilizando a regra de Simpsons encontraremos
Resposta
Exercícios de Livros Relacionados
Expresse a integral como um limite de somas. Não calcule o limite. 30 . ∫ 1 10 ( x - 4 ln x ) d x
Encontre uma aproximação para a integral ∫ 0 4 x 2 - 3 x d x usando uma soma de Riemann com as extremidades direitas e n = 8 . (b) Faça um diagrama como a Figura 3 para ilustrar a aproximação da parte
Um tronco de 10m de comprimento é cortado a intervalos de 1m e as suas áreas de secção transversal A (a uma distância x da extremidade do tronco) estão listadas na tabela. Use a Regra do Ponto Médio c
Há um fluxo de água para dentro e para fora de um tanque de armazenamento. A seguir, temos um gráfico que mostra a taxa de troca r t do volume de água no tanque, em litros por dia. Se a quantidade de
A velocidade de um carro foi lida de seu velocímetro em intervalos de 10 segundos e registrada na tabela. Use a Regra do Ponto Médio para estimar a distância percorrida pelo carro.