Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.4 - Ex. 63
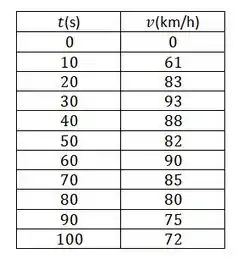
A velocidade de um carro foi lida de seu velocímetro em intervalos de segundos e registrada na tabela. Use a Regra do Ponto Médio para estimar a distância percorrida pelo carro.
Passo 1
Galera, nessa questão temos uma tabela com a velocidade do carro medida a cada até um intervalo total de .
O que o enunciado nos pede é uma estimativa para a distância percorrida pelo carro nesses .
Vamos lá, sabemos que se um objeto move-se ao longo de uma reta com função posição , teremos que velocidade é a derivada da sua posição, portanto:
Dessa forma, podemos dizer que a variação da sua posição é a integral da velocidade:
Temos que essa integral representa a mudança de posição, ou seja, o deslocamento da partícula durante o período de tempo a .
Mas como queremos a distância percorrida pelo carro, devemos ter essa integral com a função velocidade em módulo:
Mas fica tranquilo, pois aqui a velocidade é sempre positiva, então você não vai precisar se preocupar com esse módulo.
Passo 2
Vamos usar agora a Regra do Ponto Médio, vamos lembrar:
No nosso exemplo, nossa variável é o tempo e a função é a velocidade, logo:
Onde é o espaçamento entre cada subintervalo e é a velocidade medida no tempo médio de cada subintervalo.
Com o intervalo , e vamos usar subintervalos, temos que , o comprimento de cada um dos intervalos é de segundos.
Como a função velocidade está em , devemos substituir esse tempo para horas.
segundos horas
E substituindo os pontos médios de cada intervalo temos:
Resposta
A distância percorrida pelo carro é de km.