Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.1 - Ex. 3
- Estime a área sob o gráfico de de a usando quatro retângulos aproximados e pontos finais direitos. Esboce o gráfico e os retângulos. Sua estimativa é subestimada ou superestimada?
- Repita a parte (a) usando os pontos finais esquerdos.
Passo 1
Oie, tudo bem? Vou tá te ajudando a resolver essa atividade hoje.
Dada a função:
Com intervalo de :
A gente precisa encontrar a área sobre esse gráfico. Para isso a gente vai utilizar uma aproximação com retângulos.
Veja abaixo o retângulo:
Ele tem um lado esquerdo, e um lado direito, além da sua base. Quando utilizamos o lado esquerdo do retângulo como o nosso valor da ‘altura’ estamos utilizando o método de pontos finais a esquerda, e quando utilizamos o lado direitos, estamos utilizando o método de pontos finais a direita.
A gente vai utilizar então para o somatório a direita, a seguinte equação:
Onde:
Onde é o intervalo de e a quantidade de retângulos.
Para o intervalo a esquerda:
A gente começa contar os nossos a partir do e vai até o ultimo, no nosso caso, temos aqui até . Os são os valores de nos lados do nosso retângulo.
Passo 2
- Vamos lá, vamos encontrar uma estimativa usando pontos finais direitos, como vamos usar retângulos temos que , assim:
- Vamos lá, vamos encontrar uma estimativa usando pontos finais esquerdos, como vamos usar retângulos temos que , assim:
Temos que:
Aqui nós sabemos que e são os limites de integração, assim:
Vamos calcular o somatório:
Aqui temos o esboço dos retângulos:
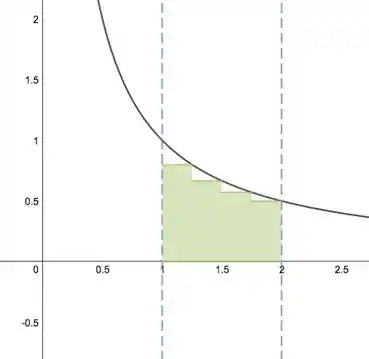
Como é decrescente em , temos uma estimativa subestimada usando a aproximação e pontos finais direitos.
Passo 3
Temos que:
Aqui nós sabemos que e são os limites de integração, assim:
Vamos calcular o somatório:
Aqui temos o esboço dos retângulos:
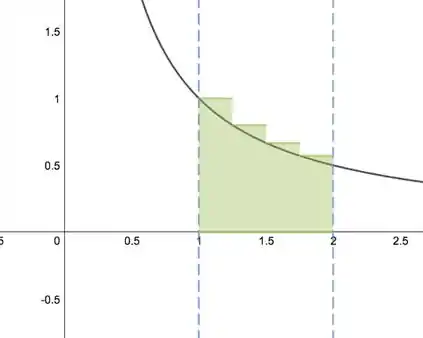
Como é decrescente em , temos uma estimativa superestimada usando a aproximação e pontos finais esquerdos.