Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.7 - Ex. 56
Uma aproximação mais precisa com os métodos de integração numérica desta seção foi obtida aumentando o número de subdivisões do intervalo. Outra estratégia é usar o mesmo
número de subintervalos, mas selecionar subintervalos de comprimentos diferentes. Discuta um esquema para fazer isso na aproximação trapezoidal de com 4 subintervalos. Comente sobre as vantagens e desvantagens desse esquema.
Passo 1
Bom, nós temos que a integral, possui um valor aproximado de . Para a aproximação trapezoidal, temos:
Calculando a aproximação que vai de a :
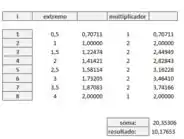
Como para o problema precisamos escolher somente subintervalos, escolhemos o que mais se aproxima do valor real da integral:
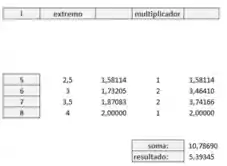
Passo 2
Comentando sobre esse resultado vemos que não chegamos ao valor exato da integral, então já se tem um erro significativo e pode interferir no processo, sendo assim uma desvantagem. No entanto, é uma vantagem pelo fato de que teremos um calculo mais rápido e fácil de se fazer!
Resposta
Vantagem: agilidade na resposta; Desvantagem: resultado nem sempre preciso.