Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.1 - Ex. 20
A tabela mostra o número de pessoas por dia que morreram de EM Singapura em intervalos de duas semanas a partir de de março de .
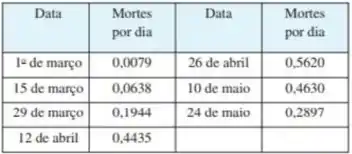
- Usando um argumento semelhante aos do Exemplo , estime o número de pessoas que morreram de em Singapura entre de março e de março de , usando ambos pontos finais esquerdos e pontos finais direitos.
- Como você interpretaria o número de mortes por como uma área sob uma curva?
Passo 1
Oie, vamos resolver mais uma atividade?
A gente tem os seguintes dados:
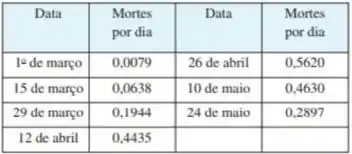
E com base no que foi feito no exemplo , onde os dados foram considerados como retângulos e utilizamos o somatório das áreas desses vários retângulos para calcularmos os dados que queremos.
Aqui a gente tem mortes/dia e temos o intervalo de dias, se realizamos o produto entre o intervalo total de dias analisado pelas mortes por dia, conseguiremos criar uma aproximação para as mortes totais.
Temos duas formas de realizarmos essas estimativas, com pontos finais a esquerda e com pontos finais a direita.
Veja abaixo o retângulo:
Ele tem um lado esquerdo, e um lado direito, além da sua base. Quando utilizamos o lado esquerdo do retângulo como o nosso valor da ‘altura’ estamos utilizando o método de pontos finais a esquerda, e quando utilizamos o lado direitos, estamos utilizando o método de pontos finais a direita.
Passo 2
- Vamos encontrar uma estimativa usando pontos finais esquerdos, e temos que , pois é o intervalo de dias, vamos então calcular:
- Podemos interpretar o número de mortes por como uma área sob uma curva que descreve a taxa de mortalidade por SARS em função do tempo.
Temos então que foram o número estimado de pessoas que morreram.
Vamos encontrar uma estimativa usando pontos finais direitos, e temos que , pois é o intervalo de dias, vamos então calcular:
Temos então que foram o número estimado de pessoas que morreram.
Passo 3
Resposta
- e
- Como uma área sob uma curva que descreve a taxa de mortalidade por SARS em função do tempo.