Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.3 - Ex. 57

Estime os intervalos de concavidade com precisão de uma casa decimal usando um sistema de computação algébrica para calcular e fazer o gráfico de f ' ' .

f x = x 3 - 10 x + 5 x 2 + 4

Passo 1

Oi meus queridos.

Nessa questão, temos a seguinte função:

f x = x 3 - 10 x + 5 x 2 + 4

E aqui podemos usar um sistema de computação algébrica para calcular e fazer o gráfico de f ' ' x .

Também vamos encontrar os intervalos de concavidade. Para isso, vamos analisar o sinal da segunda derivada.

Passo 2

Primeiro, eu vou encontrar a primeira derivada, usando um programa de computação, temos que:

f ' x = 2 x 4 + 12 x 2 - 5 x - 40 x 2 + 4 3 / 2

Por meio de um sistema computacional, temos o gráfico de f ' (a derivada primeira de f ):

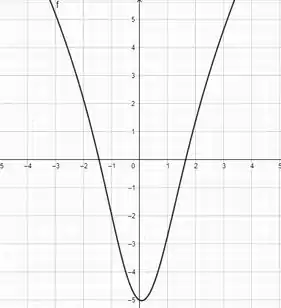
Agora vou derivar novamente e obter a segunda derivada:

f ' ' x = 2 x 5 + 10 x 3 + 5 x 2 + 108 x - 10 x 2 + 4 5 / 2

E a derivada segunda, ou gráfico de f ' ' :

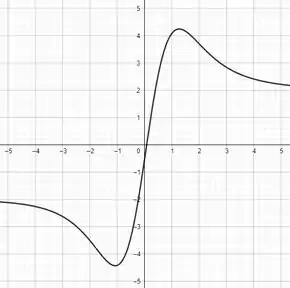
Passo 3

Se quando a derivada segunda de uma função é positiva, a concavidade é voltada para cima; e negativa a concavidade é voltada para baixo. Então a concavidade é para cima em ( 0,1 ,     ∞ ) e para baixo em ( - ∞ ,     0,1 ) .

Resposta

A concavidade é para cima em ( 0,1 ,   ∞ ) e para baixo em ( - ∞ ,   0,1 ) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nick começa trotando e corre cada vez mais rápido por 3 minutos, então ele caminha por 5 minutos. Ele para em um cruzamento por 2 minutos, corre rapidamente por 5 minutos e depois caminha por 4 minuto
A temperatura da água afeta a taxa de crescimento da truta. A tabela mostra a quantidade de peso adquirida pela truta após 24 dias em várias temperaturas da água. Se W ( x ) for o ganho de peso na tem
Quando você abre uma torneira de água quente, a temperatura T da água depende de quanto tempo a água está fluindo.(a) Esboce um gráfico possível de T em função do tempo t que decorreu desde que a torn
O gráfico da função y = f ( x ) é mostrado a seguir. Em que pontos as seguintes sentenças são verdadeiras?a) d y d x e d 2 y d x 2 são ambas positivas.b) d y d x e d 2 y d x 2 são ambas negativas.c) d
Esboce o gráfico de uma função que satisfaça a todas as condições dadas. f ' x0 para todo x ≠ 1 Assíntota vertical x = 1 f ' ' x0 e x1 ou x3 f ' ' x0 se 1x3