Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.8 - Ex. 65
Nick começa trotando e corre cada vez mais rápido por minutos, então ele caminha por minutos. Ele para em um cruzamento por minutos, corre rapidamente por 5 minutos e depois caminha por minutos.
a) Esboce um gráfico possível da distância que Nick percorreu após minutos.
b) Esboce um gráfico de .
Passo 1
E aí! tudo certinho?
Nesse problema foi descrito o comportamento de uma pessoa ao fazer exercícios na rua onde para cada intervalo de tempo, o enunciado nos deu um certo comportamento da pessoa.
Com essas informações queremos esboçar o gráfico da distância em relação ao tempo e tambem o gráfico de .
Parece complicado?
Bom galera, para fazer o gráfico espaço pelo tempo do Nick, a gente vai dividir o passeio dele em movimentos.
A partir desses movimentos, podemos esboçar o gráfico de .
Já para esboçar o gráfico de , temos que ter em mente uma propriedade da derivada que diz que a derivada de uma função pode ser interpretada como a inclinação instantânea de função, mas no caso da aplicação em uma função movimento, a derivada resulta na velocidade.
Lembra disso? Bora começar!
Passo 2
No primeiro movimento, a pessoa está acelerando, então cada vez mais ela percorre um espaço maior...
No segundo movimento a velocidade é constante, então graficamente a função é linear em relação ao tempo.
No terceiro movimento a pessoa está parada, então nesse intervalo a função é constante...
No quarto movimento a pessoa volta a correr com velocidade constante, então novamente nesse intervalo a função é linear.
Por ultimo, no quinto movimento a pessoa anda com velocidade constante, então esse intervalo tambem é linear, mas com uma inclinação menor...
Com isso o gráfico fica:
Onde o eixo é a distancia e o eixo é o tempo
Show? Bora continuar!
Passo 3
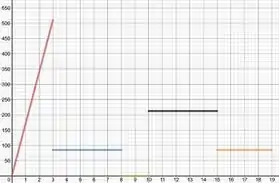
Beleza, agora vou te contar um segredo, a derivada da função do espaço pelo tempo, dá a velocidade pelo tempo, então para cada um dos movimento temos uma derivada diferente, vamos usar valores inventados de velocidade.
No primeiro movimento, é dito que a pessoa está acelerando continuamente, logo, sua velocidade cresce linearmente com o tempo.
No segundo movimento a velocidade é constante e relativamente baixa.
No terceiro movimento, a pessoa para, nesse intervalo a função velocidade é nula.
No quarto movimento a pessoa corre com velocidade constante e alta.
E no ultimo movimento, a pessoa continua correndo com velocidade constante, porem mais devagar...
Como onde é a velocidade, temos que o gráfico da derivada de é dada por
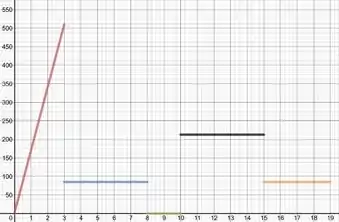
Onde o eixo é a velocidade e o eixo é o tempo.
E aí! entendeu tudo? Responde Aí!
Resposta
a)
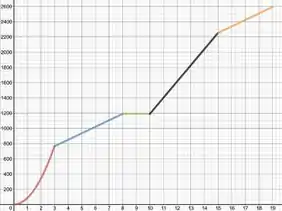
b)
