Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.3 - Ex. 33

Estime o valor de

fazendo o gráfico da função

Faça uma tabela de valores de para próximo de e estime qual será o valor do limite.

Use as propriedades dos Limites para encontrar o valo exato do limite.

Passo 1

Eaee, belezinha?? Bom... queremos estimar o valor do seguinte limite fazendo o gráfico de :

Para isso, deveremos plotar e analisar o que acontece quando tende a zero.

O enunciado também nos pede para fazer uma tabela de valores de para próximo de e estimar qual será o valor do limite.

Também deveremos utilizar as propriedades dos limites para encontrar o valo exato do limite, pois não podemos apenas faze porque geraria uma indeterminação, veja:

Assim, a gente vai fazer algumas manipulações algébricas!! 😉

Passo 2

Vamos analisar o plot do gráfico da função:

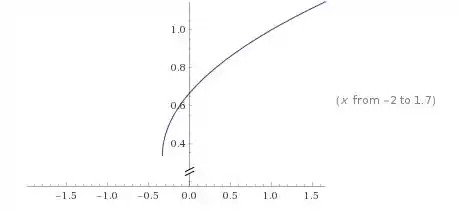
Vamos observar o que acontece quando se aproxima do valor , o valor pedido no limite: pela direita podemos ver que a função vai se aproximando mais e mais do valor , e o mesmo ocorre pela esquerda.

Então podemos ver que o valor da função quando está se aproximando mais e mais de , tando pela direita quanto pela esquerda, é .

Passo 3

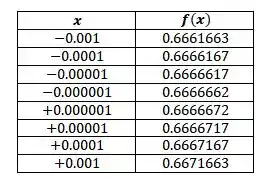
Para estimar o limite através de uma tabela de valores de vamos atribuir valores de bem próximos a , e observar para qual valor eles convergem, vamos lá:

Pela tabela podemos observar que o valor do limite parece se aproximar de , viu, não é complicado! :)

Passo 4

Agora vamos encontrar o valor exato do limite através das propriedades:

Vamos fazer uma tentativa multiplicando tanto o numenador quanto o denominador pelo conjugado do denominador da expressão, , e resolver a multiplicação do denominador:

Passo 3

Agora sim podemos usar algumas propriedades, vamos lá:

Mas antes disso valor simplificar a expressão, eliminando o termo que aparece tanto no numerador quanto no denominador:

Vamos usar três propriedades: primeiro vamos tirar a constante que está multiplicando a função para fora do limite, depois usar a propriedade da soma, e por último tirar a raíz da função colocando o limite dentro da raiz, você vai ver que vai ficar mais simples resolver depois disso: