Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.3 - Ex. 34
a) Use o gráfico de
para estimar o valor de com duas casas decimais.
b) Utilize uma tabela de valores de para estimar o limite com quatro casas decimais.
c) Use as Propriedades dos Limites para encontrar o valor exato do limite.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente usar o gráfico da função para estimar o valor do limite com duas casas decimais. Depois, devemos utilizar uma tabela de valores de para estimar o limite com quatro casas decimais. E por fim, devemos encontrar o valor exato do limite usando as propriedades dos limites.
Então, podemos usar um software ou uma calculadora gráfica para esboçar o gráfico de . Assim, podemos analisar os valores de bem próximos de e verificar para onde parece que a nossa função está convergindo.
Em seguida, vamos atribuir alguns valores de , também bem próximos de , calcular o valor de para cada um desses valores e construir uma tabela com ele. Dessa forma, vamos poder observar na tabela o valor que estará se aproximando à medida que se aproxima de zero.
Por último, vamos calcular o limite usando as seguintes propriedades dos limites, de maneira a fugir da indeterminação e aplicar o valor na expressão.
Vamos lá!
Passo 2
(a) Vamos começar plotando o gráfico da função no plano cartesiano, com o auxílio de um software. Assim, temos:
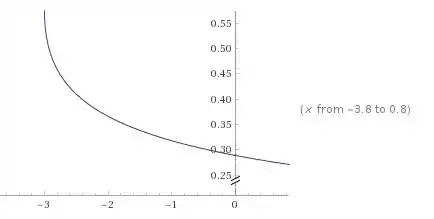
Vamos observar o que acontece quando se aproxima do valor , o valor pedido no limite:
Pela direita podemos ver que a função vai se aproximando cada vez mais do valor , e o mesmo ocorre pela esquerda.
Então podemos ver que o valor da função quando está se aproximando mais e mais de , tanto pela direita quanto pela esquerda, é .
Passo 3
b) Para estimar o limite através de uma tabela de valores de vamos atribuir valores de bem próximos a , e observar para qual valor eles convergem, vamos lá:
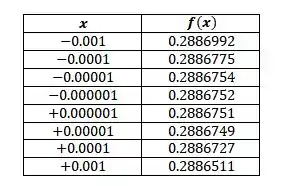
Pela tabela podemos observar que o valor do limite parece se aproximar de , considerando quatro casas decimais após a vírgula.
Passo 4
c) Agora vamos encontrar o valor exato do limite através das propriedades. Nosso limite é dado por:
Observe que apenas substituindo na função, teríamos uma indeterminação do tipo . Então, temos que fugir dela. Para isso, vamos começar multiplicando tanto o numenador quanto o denominador pelo conjugado do numenador da expressão, que é . Assim, vamos ter:
Aplicando a propriedade distributiva nos produtos:
Simplificando, obtemos:
Ainda dá pra simplificar, eliminando o termo que aparece tanto no numerador quanto no denominador:
Passo 5
Agora vamos usar as propriedades do limite que nos dizem que o limite de uma divisão é igual a divisão dos limites e que o limite da soma é igual a soma dos limites (para o denominador):
Vamos agora tirar a raíz da função do denominador colocando o limite dentro da raiz, você vai ver que vai ficar mais simples resolver depois disso:
Agora é só substituir o valor na expressão e pronto!
E encontramos o valor exato do nosso limite.
Valeu, galera! Até a próxima! 😉
Resposta
a)
b)
c)