Estime o valor do limite (se existir) pela avaliação da função nos números dados (usar 6 casas decimais).
Passo 1
Bom pessoal, para existir o limite, a função deve tender a um certo valor tanto pela esquerda quanto pela direita.
A questão nos pede para encontrar o limite da função avaliando os valores da função. Isso significa que iremos calcular os valores de para
E descobrir para qual valor ela caminha a medida que nos aproximamos de .
Passo 2
Agora sim, vamos pegar a calculadora:
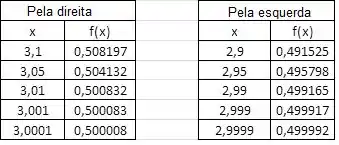
Vemos então que a tendência do limite é igual a ½.