Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.1 - Ex. 7

A tabela mostra a posição de um ciclista

Encontre a velocidade média nos períodos de tempo a seguir:

[1,3]

[2,3]

[3,5]

[3,4]

Use o gráfico de s como uma função de t para estimar a velocidade instantânea quando t = 3 .

Passo 1

Olá, meus amores!

Aqui o que devemos fazer é calcular a velocidade média nos tempos dado. Lembrando que a velocidade média tem essa fórmula aqui:

v m e d = s t 2 - s t 1 t 2 - t 1

É a variação da posição s dividida pela variação do tempo t . O negócio é simplesmente pegar os intervalos dados e calcular a velocidade pra cada um deles, considerando os 2 pontos de cada intervalo. Hmmm, não entendeu? Você já vai entender e ver que é moleza!

Depois nós vamos traçar o gráfico da posição pelo tempo, que basicamente é plotar os dados da tabela. E desta curva, vamos estimar a velocidade em t = 3 .

Um pouco complicado? Confia que é mais facil do que parece.

Passo 2

Como já vimos no passo 1, pra calcular as velocidades médias, faremos

v m e d = s t 2 - s t 1 t 2 - t 1

Relembrando a tabela:

No intervalo [1,3], temos os pontos:

( 1   ; 1 , 4 )

( 3   ; 10,7 )

Então a velocidade fica:

v m e d = 10,7 - 1,4 3 - 1 = 9,3 2 = 4,65   m / s

No intervalo [2,3], temos os pontos:

( 2   ; 5,1 )

( 3   ; 10,7 )

Então a velocidade fica:

v m e d = 10,7 - 5,1 3 - 2 = 5,6 1 = 5,6   m / s

No intervalo [3,5], temos os pontos:

( 3   ; 10,7 )

( 5   ; 25,8 )

Então a velocidade fica:

v m e d = 25,8 - 10,7 5 - 3 = 15,1 2 = 7,55   m / s

No intervalo [3,4], temos os pontos:

( 3   ; 10,7 )

( 4   ; 17,7 )

Então a velocidade fica:

v m e d = 17,7 - 10,7 4 - 3 = 7 1 = 7   m / s

Passo 3

Esboçando o gráfico, ficamos com

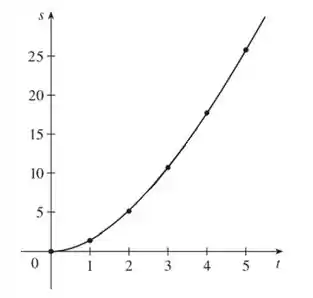
A velocidade instantânea em t = 3   é dada pela inclinação da reta tangente à curva no ponto t = 3 . Então vamos começar traçando essa reta tangente:

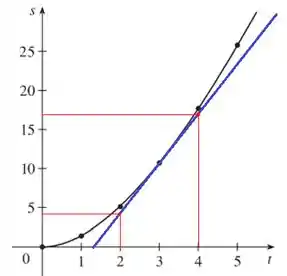
E pra calcular sua inclinação precisamos de 2 pontos da reta e eu escolhi esses 2 marcados no gráfico:

2   ,   4

( 5   ,   23 )

LEMBRE-SE QUE SÃO PONTOS DA RETA E NÃO DA CURVA! AQUI QUEREMOS ACHAR A RETA!

Jogando esses pontos na fórmula da velocidade instantânea:

v i n s t a n t a n e a = s t 2 - s t 1 t 2 - t 1

v i n s t a n t a n e a = 23 - 4 5 - 2 = 19 3 ≈ 6,3   m / s

Note que usamos dois pontos quaisquer, outros também poderiam ser usados (desde que da reta).

Resposta

Para [1,3]

v m e d = 4,65   m / s

Para [2,3]

v m e d = 5,6   m / s

Para [3,5]

v m e d = 7,55   m / s

Para [3,4]

v m e d = 7   m / s

v i n s t a n t a n e a ≈ 6,3   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula se move ao longo de uma reta com equação de movimento s = f ( t ) , em que s é medido em metros e t em segundos. Encontre a velocidade e a velocidade escalar quando t = 5 . f t = t - 1 -
Se um tanque cilíndrico comporta 100000 litros de água, que podem escoar pela base do tanque em uma hora, então a Lei de Torricelli fornece o volume V de água que restou no tanque após t minutos como:
O custo da produção de x quilogramas de ouro provenientes de uma nova mina é C = f ( x ) dólares. Qual o significado da derivada f ’ ( x ) ? Quais são suas unidades? O que significa f‘ ( 50 ) = 36 ? V
O custo (em dólares) de produzir x unidades de uma certa mercadoria é C x = 5000 +10 x + 0,05 x 2 a) Encontre a taxa média da variação de C em relação a x quando os níveis de produção estiverem varian
Seja T ( t ) a temperatura (em ° C ) em Seul t horas após o meio-dia em 21 de agosto de 2004 . A tabela mostra os valores dessa função registrados de duas em duas horas. Qual o significado de T ‘ ( 6