Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 9.6 - Ex. 9
No Exemplo 1(b) mostramos que as populações de coelhos e lobos satisfazem a equação diferencial
Resolvendo essa equação diferencial separável, mostre que
Onde é uma constante.
É impossível resolver essa equação para como uma função explícita de (ou vice-versa). Se você tiver um sistema de computação algébrica que trace curvas definidas implicitamente, use essa equação e seu SCA para denhar a curva solução que passa pelo ponto e compare com a Figura 3.
Passo 1
Precisamos resolver a equação diferencial
Como se trata de uma equação separável, vamos jogar todos os termos com para um lado e os com para o outro lado. Se liga aí:
Vamos dividir a equação inteira por
Agora vamos dividir a equação toda por L:
Passo 2
Integrando ambos os lados...
Onde é a nossa famosa constante de integração.
Quando chegamos nesse ponto da resolução os logaritmos estão incomodando, então vamos lembrar de algumas propriedades para melhorar nossa vida:
Agora podemos aplicá-las na nossa equação:
Agora vamos também lembrar de uma propriedade de potências:
Vamos chamar e substituir na nossa equação, isolando
Passo 3
Agora queremos desenhar, através de algum site (podemos utilizar o WolframAlpha, Desmos ou Geogebra para fazer isso) uma curva que use essa solução e passe pelo ponto . Nosso gráfico fica assim: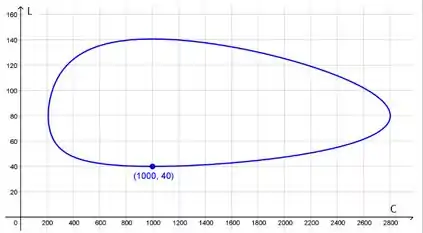
Resposta
Ei, a resposta está no passo a passo :)