Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 11.10 - Ex. 42
Encontre a série de Maclaurin de (por qualquer método) e seu raio de convergência. Trace e seus primeiros polinômios de Taylor na mesma tela. O que você observa sobre a relação entre esses polinômios e ?
Passo 1
Fala, time! Tudo tranquilo?
A questão quer que a gente encontre a série de Maclaurin de :
Achar a série de Maclaurin de uma função é expressá-la como uma soma infinita de termos (série) calculados a partir de suas derivadas em um ponto, que aqui para as séries de Maclaurin é . A série de Maclaurin nada mais é que a série de Taylor com e é assim:
Olhando nosso formato de série vemos que o que falta encontrarmos é justamente que são as derivadas de no ponto zero vezes. Encontrando esse termo, nós substituímos em e temos nossa série de Maclaurin pra função que o enunciado pede.
Acontece que geralmente precisamos ter esse trabalho todo com séries de Taylor centradas em outros valores de . Para , temos as séries de Maclaurin e já temos essas séries tabeladas e prontas na teoria do nosso livro, inclusive com seus raios de convergência .
Nesse caso aqui, embora o livro traga que o raio de convergência de nossa função tem um argumento diferente de , que no nosso caso é , então vamos precisar calcular o . Achar esse valor é achar para quais valores de nossa série converge. E para isso vamos usar o Teste da Razão, que facilita bastante nossos processos quando temos termos fatoriais, que é o caso da série de Maclaurin. Relembrando o Teste da Razão: calculamos o limite:
Se: a série é absolutamente convergente (e, portanto, convergente). Se a série é divergente (o mesmo para )e se o teste é inconclusivo.
Por fim a questão pede para traçarmos os polinômios de Taylor da série, que nada mais são que os próprios termos da série, que são do formato de polinômios de .
Traçamos esses polinômios e a nossa função e observamos o comportamento dessas curvas.
Bora resolver isso!
Passo 2
Olhando na nossa teoria (Tabela 11 da sessão 11.10), sabemos que a série de Maclaurin para é:
Mas como queremos a série de Maclaurin para , vamos substituir nosso por :
Aplicando a propriedade da potenciação: , simplificamos para:
Então, a série acima é a Série de Maclaurin de .
Passo 3
Agora precisamos encontrar o raio de convergência da nossa série:
E para isso vamos usar o teste da razão. Teremos:
E fazendo :
Simplificando os expoentes de na série acima:
Ficamos com:
Aplicando o teste da razão, já vamos expressão a divisão de frações como a multiplicação da primeira fração pelo inverso da segunda:
Para simplificar nosso termo dentro do limite, vamos abrir as somas nos expoentes com a propriedade da potenciação:
Simplificando os termos iguais que estão sendo divididos:
Novamente simplificando, já podemos também retirar os termos que não dependem do de dentro do módulo, sendo que vai sair positivo. Mantemos o módulo no :
Para simplificar nossa análise, vamos dividir o numerador e o denominador por :
O teste da razão diz que a série converge quando . No caso temos:
Tirando a raiz sexta da inequação:
E o raio de convergência? Como a série converge para o raio de convergência é . 😉
Passo 4
Alguns polinômios de Taylor da série:
são:
Com :
Até :
Até :
Até :
Traçando o gráfico de e alguns polinômios de Taylor no software GeoGebra, vemos que nos dá uma aproximação de próxima a 0 conforme cresce.
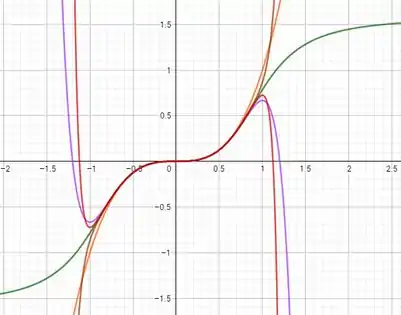
Nossa função:
Está em verde e os polinômios nas demais cores. Quanto maior o grau do polinômio (expoente ), mais o polinômio se aproxima do formato de na região da origem .
Resposta
O raio de convergência é .