No exemplo , mostre que outra equação que define em termos de é:
Use essa equação para determinar a que distância da parede o observador deve ficar para conseguir a melhor visão do quadro.
Passo 1
A figura que ilustra a situação é essa aqui:
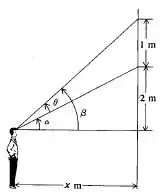
Pelos ângulos que ele deu, temos que:
E
Pela fórmula da subtração de arcos, vamos ter:
Logo:
Agora, usando a definição de
Passo 2
Para acharmos a melhor visão, devemos achar o ângulo máximo. Para isso, devemos olhar a derivada de
Vamos fazer
Com
Só para organizar as nossas contas.
Vamos ter
Temos
Que é a derivada de
Então
Passo 3
Vamos finalizar achando a derivada de . Para isso vamos usar a regra do quociente:
Vamos ter
Passo 4
Vamos analisar o sinal dessa derivada agora para uisarmos o teste da priemira derivada:
O denominador vai ser sempre positivo, porque é a soma de dois números ao quadrado.
Então o sinal depende só de , vamos olahr seu gráfico para entender como ela vai se comportar:
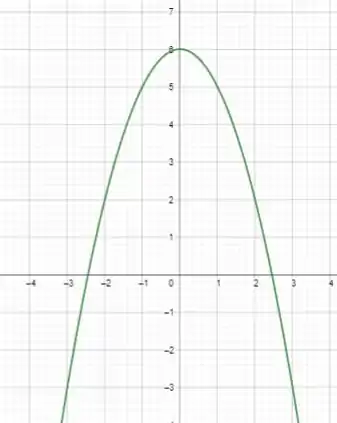
Entre as raízes vai ser positivo e antes ou depois delas vai ser negativo.
Estamos procurando um ponto de máximo, ou seja, quando a derivada é positiva antes do ponto e negativa depois.
Olhando o gráfico isso vai acontecer na rais da direita, vamos encontra-la
Como queremos a da direita, vamos ter
E essa é a distância que ele deverá ficar
Resposta
Ei, a resposta está no passo a passo :)