1. Na ausência de joaninhas, na primeira equação e o equilíbrio será alcançado quando

Onde teremos duas soluções possíveis: ou disso .

Então, quando não tivermos joaninhas, a população de pulgões ficará estável em 10000.

Passo 2

2. Para encontrarmos as soluções de equilíbrio, precisamos encontrar os valores de e para os quais e .

Bom, vamos analisar quando

Isso implica que

é uma solução (i)

Para encontrar a outra solução vamos dividir ambos os lados da equação por , então:

Vamos multiplicar a equação toda por agora para facilitar nossas contas:

(ii)

Agora vamos analisar quando , então teremos mais duas soluções:

é uma das soluções(iii)

Para encontrar a outra solução, vamos dividir ambos os lados por , ficamos com:

(iv)

Agora vamos ver o que significam todos esses resultados. Nós temos quatro possíveis soluções:

1. Equações (i) e (ii) Quando
2. Equações (i) e (iv) Quando (essa resposta não faz sentido, pois uma população não pode ter dois valores diferentes ao mesmo tempo.)
3. Equações (ii) e (iii) Quando e

Substituindo ficamos com

4. Equações (ii) e (iv) Quando e

Substituindo , ficamos com

Resumindo: nós temos três soluções de equilíbrio:

e

e

Passo 3

3. Queremos uma expressão para , ou seja, uma descrição de como a população de joaninhas varia em função da população de pulgões.

Usando a regra da cadeia, nós podemos escrever:

x

A boa notícia é que o problema nos forneceu e , basta substituirmos na fórmula:

Passo 4

4. Precisamos usar um sistema de computação algébrica para desenhar um campo de direções para a equação diferencial na parte (c). Ficamos com o campo:



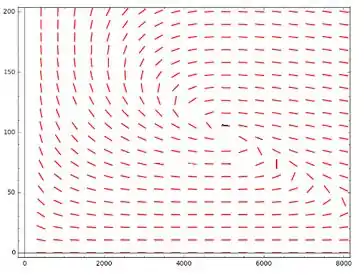
Nosso retrato de fase fica:



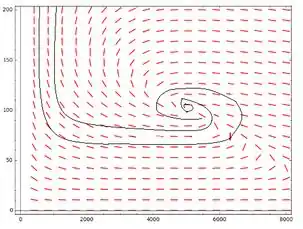
Em comum podemos ver que a solução de equilíbrio e está dentro de todas as fases.

Passo 5

5. Neste item, podemos usar o campo de direções do item anterior para desenhar a rajetória correspondente para quando inicialmente temos pulgões e joaninhas. Basta marcar esse ponto no gráfico e traçar a curva seguindo as direções:



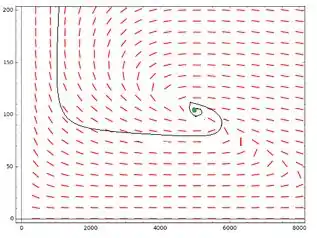
Passo 6

6. Vamos usar a parte (e) para fazer esboços das populações de pulgões e joaninhas como funções de t:

A relação existente entre os gráficos é que eles possuem o mesmo período.