Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 7.1 - Ex. 54
No Exercício 6 da Seção 6.2, giramos em torno do eixo a região entre a curva e o eixo de a para gerar um sólido de volume . Em vez disso, se girarmos a região em torno do eixo , que volume obteremos? (Veja o gráfico no Exercício 6 da Seção 6.2)
Passo 1
Precisamos obter o volume de um sólido de revolução formado pela rotação de uma região em torno do eixo . Vamos relembrar então como foi ensinado lá na Seção 6.1, pelo método do disco. Lá, aprendemos que, o volume de um sólido é dado pela seguinte integral:
Em que e são os limites inferior e superior de integração (valores mínimo e máximo de ), respectivamente, e é a função que descreve o raio dos discos transversais ao eixo de rotação, que no nosso caso é o eixo . Portanto, só precisamos definir quem são os limites e qual é a nossa função .
Passo 2
Para nos auxiliar na visualização da região, vamos esboça-la abaixo.
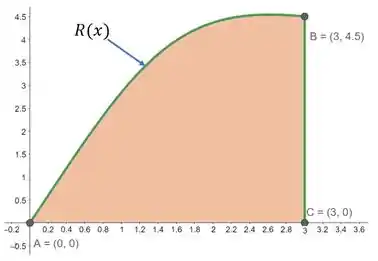
Em destaque temos a região limitada pelas curvas. Temos que identificar quem é a função .
Passo 3
A função é aquela que determina o raio de cada disco transversal ao eixo . Coincidentemente, ele é a curva que limita superiormente a nossa região. Desta forma, a função corresponde a nada mais e nada menos que:
Já para descobrirmos os limites de integração, basta nós respondermos a seguinte pergunta: quais são os valores mínimo e máximo que assume? Olhando para o esboço no Passo 2, fica claro que são e , a origem do sistema de coordenadas e a curva que limita nossa região à direita.
Passo 4
Temos todas as informações necessárias para calcularmos o volume do nosso sólido. Desta forma, temos:
Para resolvermos esta integral, vamos fazer uma mudança de variáveis. Chamando , temos . Já em relação aos limites, quando e quando . Portanto, temos: