Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.1 - Ex. 1m

1 - Calcule o volume do sólido obtido pela rotação, em torno do eixo x , do conjunto de todos os pares x ,   y tais que

M - x 2 + y - 2 2 ≤ 1

Passo 1

Poxa! Que tal aqui começarmos o nosso problema desenhando a nossa região...

x 2 + y - 2 2 ≤ 1

Poxa, a equação x 2 + y - 2 2 = 1 representa uma circunferência de raio 1 e centrada no ponto 0 ,   2 - deslocada duas unidades em y :

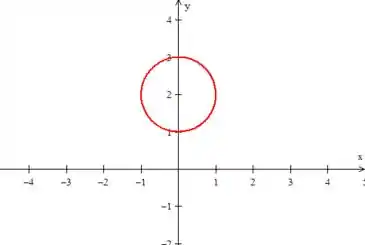
Como temos o sinal de menor na inequação: x 2 + y - 2 2 ≤ 1 , isso significa que queremos a região no interior da circunferência:

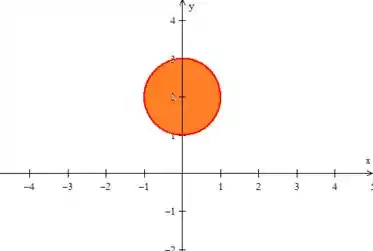
Então quando a gente girar esse treco ao redor de x , vamos obter um pneu com o eixo em x , saca? Sabemos que o volume de revolução de uma curva pode ser obtido como...

V = π ∫ a b f x 2 - g x 2   d x

Bora ver quem são cada um desses elementos então!

Passo 2

Primeiro, vamos para os limites: a ,   b . Bem, a é o ponto mais a esquerda da curva enquanto que o b o extremo da direita.

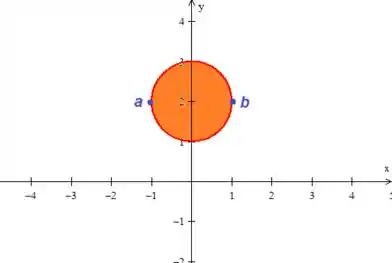
Então a = - 1 e b = 1 .

f x é função que representa a curva de cima (em verde) enquanto que g x é a curva de baixo, em amarelo:

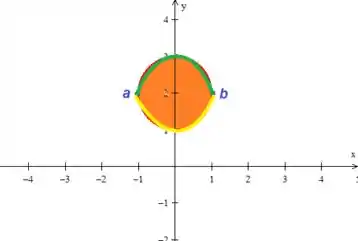
Ambas curvas podem ser obtidas da equação da circunferência isolando o y :

x 2 + y - 2 2 = 1 →

y - 2 = ± 1 - x 2   →

y = 2 ± 1 - x 2

Então...

f x = 2 + 1 - x 2               e             g x = 2 - 1 - x 2

Passo 3

Agora é só substituir...

V = π ∫ a b f x 2 - g x 2   d x     →

V = π ∫ - 1 1 2 + 1 - x 2 2 - 2 - 1 - x 2 2   d x       →

V = π ∫ - 1 1 4 + 4 1 - x 2 + 1 - x 2 - 4 - 4 1 - x 2 + 1 - x 2   d x       →

Simplificando...

V = π ∫ - 1 1 8 1 - x 2   d x       →

Que tal substituirmos x por cos ⁡ t ?

x = sin ⁡ t       →           d x = cos ⁡ t d t

Não se esqueça de trocar os limites também:

- 1 = sin ⁡ t       →           t = - π 2

1 = sin ⁡ t       →           t = π 2

V = π ∫ - 1 1 8 1 - x 2   d x               →               V = 8 π ∫ - π 2 π 2 1 - sin ⁡ t 2   cos ⁡ t d t     →

Como cos ⁡ t = 1 - sin ⁡ t 2 ...

V = 8 π ∫ - π 2 π 2 cos 2 ⁡ t d t

Poxa, sabemos que...

cos 2 ⁡ t = 1 + cos ⁡ 2 t 2

Então...

V = 8 π ∫ - π 2 π 2 1 2 + cos ⁡ 2 t 2 d t   →

V = 8 π 1 2 t + sin ⁡ 2 t 4 - π 2 π 2   →

O volume então é dado por...

V = 8 π 1 2 π 2 - sin ⁡ π 4 - 1 2 - π 2 - sin ⁡ - π 4   →

V = 8 π π 2   →

4 π 2

Resposta

V = 4 π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 1 em torno de A B .
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 2 em torno de O C .
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 1 em torno de B C .
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 3 em torno de O A .
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = x + 1 ,y = 0 , x = 0 , x = 2 ;