Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.3 - Ex. 6
No exercício a seguir, comprove o teorema do valor médio para a equação dada no intervalo indicado. Ache então um valor “c” que satisfaça a conclusão do teorema do valor médio
Passo 1
Bom galera, temos que trabalhar neste exercício com o teorema do valor médio. Ele é bem mais simples do que parece, e vamos esclarecer aqui rapidinho algumas coisas sobre ele, tá bom? Ele funciona da seguinte forma:
Seja uma função f tal que:
- Ela seja contínua no intervalo fechado [a,b]
- Ela seja derivável no intervalo aberto (a,b)
Então exite um número c no intervalo aberto (a,b), tal que:
Não entendeu nada? Calma... vamos mastigar esse teorema JUNTOS!
Passo 2
A primeira hipótese fala da função ser continua no intervalo fechado [a,b]. Como é uma função polinomial super de boas, a gente sabe que: não só ele é continuo no intervalo fechado [a,b], como também é DERIVÁVEL no intervalo abeto (a,b), porque toda função polinomial não racional, existe em todo o eixo x... então... QUE BOOOOOOM! Não está convencido(a) ainda? Vamos para o gráfico então:
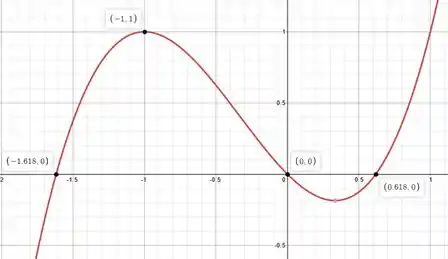
Tá vendo galerinha? A gente pode ver claramente que a função é contínua e derivável no nosso intervalinho dado!!
Passo 3
Agora neste passo, iremos nos concentrar em comprovar a parte do teorema que diz que para a nossa função, exite:
Vamos lá! Nossa função aplicada em a:
Agora para nossa função aplicada em b:
Portanto, nosso f’(c):
Passo 4
Agora precisamos equacionar nossa função derivada em c, para achar o valor de c e enfim terminar nossa questão. Vamo lá! Primeiro derivar nossa função e igualar ao valor de f’(c) = 3.
E as raízes dessa equação resultam em:
E esses dois pontos , estam no intervalo de ! Logo, TEOREMA MASTIGADO, DESTRUÍDO E PROVAAAADO!
Resposta
Ei, a resposta está no passo a passo :)