Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 7b
Nos Exercícios 1-10, determine os volumes dos sólidos.
7- A base de um sólido é a região limitada pelos gráficos de , e . As seções transversais perpendiculares ao eixo são
- Retângulos de perímetro 20
Passo 1
É bom fazermos um esboço da região que queremos, que pode ser vista abaixo:
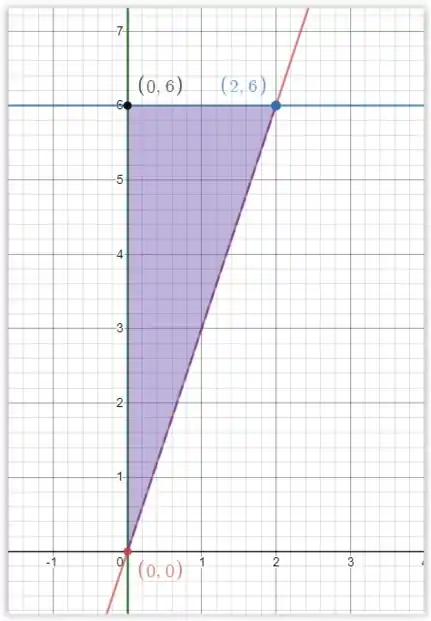
Passo 2
Fala-se na questão que o retângulo transversal a figura tem perímetro de 20, logo precisamos encontrar sua altura para podermos calcular a área. Então calculando o perímetro temos:
Onde a base é
Como temos agora a altura vamos calcular a área
Passo 3
Pela figura precisamos saber ver e saber calcular a variação de , que vai de 0 a 2, e que integrando a área que acabamos de calcular ela vai nos fornecer o volume do sólido:
Substituindo os valores encontramos:
Resposta
Exercícios de Livros Relacionados
Conforme a figura abaixo, um copo de coquetel com a forma de um hemisfério com diâmetro de 8c m contém um cereja com 2c m de diâmeto. Se o copo for preenchido até uma profundidade de hc m , que volume
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O método das camadas cilíndricas é um caso especial do método de integração de áreas de seções transversais discutido na Seçã
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O volume de uma camada cilíndrica é igual ao produto da espessura da camada com a área de superfície do cilindro cuja altura
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo y . y = x , x = 4 , x = 9 , y = 0