Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 3

Nos Exercícios 1-10, determine os volumes dos sólidos.

3-

O sólido está situado entre planos perpendiculares ao eixo x em x = - 1 e x = 1 . As seções transversais perpendiculares ao eixo x entre esses planos são quadrados cujas bases se estendem do semicírculo y = - 1 - x 2 ao semicírculo y = 1 - x 2

Passo 1

Para ajudar no entendimento um desenho sempre é válido:

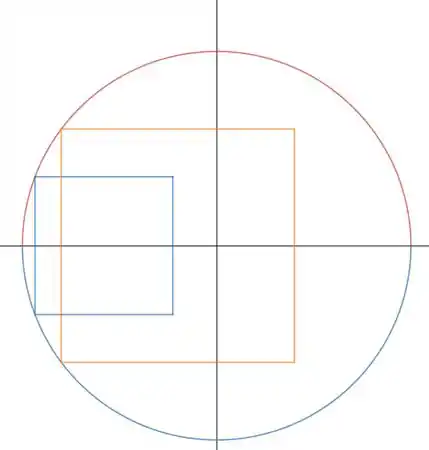
Onde a questão diz com outras palavras que temos vários quadrados que percorrem um círculo de modo que uma resta aumente o seu lado como indo do quadrado azul para o laranja.

E temos que a área do quadrado de lado A é:

A = a 2

Passo 2

O nosso cálculo precisa estar em função de x então podemos dizer que a aresta do quadrado é a distância entre um semicírculo para outro.

A = 1 - x 2 - ( - 1 - x 2 2

Logo:

A = 2 1 - x 2 2 = 4 ( 1 - x 2 )

Passo 3

Como o quadrado faz esse percurso indo do ponto x = - 1 ao x = 1 temos que a integral nesse intervalo nos dá o volume nesse mesmo intervalo:

V = ∫ - 1 1 4 1 - x 2

Logo:

V = 4 x - x 3 3 - 1 1

V = 4 1 - 1 3 - 4 - 1 - - 1 3

V = 4 2 3 - 4 - 1 + 1 3

V = 8 3 - 4 - 2 3

V = 8 3 + 8 3 = 16 3

Resposta

V = 16 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se um fluido entra em um tanque semiesférico com raio de 3m , a uma taxa de 0,5m 3 / m i n , com que velocidade estará subindo quando a profundidade for de 1,5m ? [Sugestão Veja o exercicio 55 .]
A figura a seguir mostra as dimensões de uma pequena lâmpada em 10 pontos igualmente espaçados.(a) Use fórmulas de Geometria para fazer uma primeira estimativa do volume englobado pela parte de vidro
A figura abaixo mostra uma calota esférica de raio ρ e altura h cortada de uma esfera de raio r . Mostre que o volume V da calota pode ser expresso como: V = 1 3 π h 2 ( 3 r - h ) V = π h 6 3 e 2 + h
Encontre o volume da cunha descrita no Exercício 61 por fatiamento perpendicular ao eixo x .
Em 1635, Bonaventura Cavalieri, um aluno de Galileu, estabeleceu o seguinte resultado, chamado princípio de Cavalierri: Se dois sólidos tiverem a mesma altura, e se as áreas de suas seções transversai